تحليل فراوانی داده ها

آخرین به‌روزرسانی: 24 دی 1401

در مقاله قبلی به بخش دوم آنالیز واریانس یک عاملی برای داده های رتبه ای پرداختیم. در این فصل به آموزش تحليل فراواني داده ها، در ادامه سری مقالات آموزشی آمار به زبان ساده می پردازیم.

داده های اسمی، گروه بندی شده و فراوانی ها

موارد زيادي از حالت هايي وجود دارد که داده ها اسمي بوده و مي خواهيم اثر متغيري مستقل را روي متغير وابسته بررسي كنيم. در اين حالت به جاي اينكه عددي نشاندهنده ي مقياسي ترتيبي و يا فاصله اي باشد بيانگر رده اي است كه آزمودني مورد نظر به آن تعلق دارد. آزمايشگري علاقه مند به بررسي طول موي دانشجويان دختر بوده و از اين رو اين متغير را به دو رده تقسيم بندي مي كند: بلند (تا زير و يا روي شانه) و كوتاه (بالاتر از شانه). پس از آن مي توان جهت بررسي برتري دختران بر حسب ميزان طول موي سر در محيط دانشگاه نمونه گيري كرد. بايد توجه داشت كه داده هاي جمع آوري شده نه از نوع نمره و نه از نوع امتياز هستند. در اين حال محقق در حال جمع آوري مجموعه فراواني داده ها است كه در آن تعداد شركت كننده ها در هر رده با هم جمع شده اند. در صورتيكه  به صورت تصادفي 100 دانشجوي دختر انتخاب شده و 62 نفر داراي موهاي بلند و 38 نفر با موي كوتاه باشند، در آن صورت مي توان نتيجه گرفت كه تفاوت معني داري براي برتري دختران برحسب بلندي موي آنها وجود دارد؟ آماره ي مورد آزمون در اين فصل يعني كاي دو (χ^2) اجازه ي تحليل مجموعه فراواني داده ها را جهت پاسخ به اين سوال مي دهد. در اين رابطه محدوديتي روي تعداد رده هاي انتخابي (متغير مستقل) وجود نداشته و از اين لحاظ آماره اي بسيار مفيد است خصوصاً زماني كه با پرسشنامه ها و يا نظرسنجي ها مواجه هستيم. اگر بخواهيم مقايسه اي روي افراد ليبرال و محافظه كار داشته باشيم، مي توان براساس يك بخش قانون مالياتي جديد از ميان ليبراهاو محافظه كاران تعداد افراد موافق و مخالف اين قانون را بدست آوريم. بنابراين چهار رده وجود دارد: ليبرال موافق، ليبرال مخالف، محافظه كار موافق و محافظه كار مخالف كه با فراواني هاي مربوطه مي باشند. اگر در هر كدام از رده هاي نوع گروه سياسي رده اي با عنوان “نمي دانم” وجود داشته باشد تعداد كل رده ها به شش تا افزايش مي يابد.

مقدمه اي بر χ^2

ساده ترين روش نشان دادن آماره ي χ^2، مربع يك آماره ي استاندارد  شده ي z است.

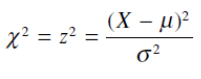
χ^2 مربع تفاضل نمرات از ميانگين يك جمعيت تقسيم بر واريانس است كه در آن توزيع جمعيت نرمال است.

چنانچه در مورد آماره ي F مشاهده شد ساده ترين حالت آن همان T^2 است كه در نتيجه اين آماره هيچگاه منفي نخواهد بود و اين امر در مورد χ^2 نيز رخ مي دهد، كه مربع يك مقدار بوده و هميشه مثبت است. مانند F در مورد توزيع χ^2 نيز بيشتر مقادير بالايي مد نظر است گرچه حتي در مواردي كه با آزموني دو طرفه روبرو باشيم هم مقدار z مثبت بزرگ و هم مقدار z منفي بزرگ در صورتيكه به توان دو برسند به يك مقدار χ^2 مثبت بزرگ تبديل مي شوند.

در بسياري از موارد به جاي آزمون كردن نمرات افراد نمونه ها را مورد بررسي قرار مي دهيم كه توزيع χ^2 در چنين تحليل داده هايي بسيار مفيد واقع مي شود. اگر نمونه هاي متقابلاً مستقل را بر اساس Xي كه داريم بدست آوريم، مشخص مي شود كه مجمع توزيع هاي جداگانه ي χ^2 نيز از توزيع χ^2 پيروي مي كند.

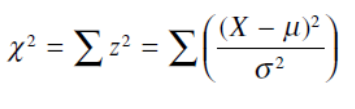
بدين معني كه براي هر نمونه مي توان χ^2 را محاسبه كرد و مجموع اين χ^2 ها نيز توزيع χ^2 خواهد بود. اين امر اجازه ي مقايسه نمونه ها را با استفاده از توزيع نمونه گيري χ^2 مي دهد. شكل توزيع χ^2 بستگي به تعداد χ^2 هايي دارد كه با هم جمع مي شوند، كه ما را هدايت به سمت محاسبه درجه آزادي نمونه ها مي كند (تعداد نمونه ها منهاي يك). اگر چهار رده بندي وجود داشته باشد درجه آزادي χ^2 برابر با c – 1 = 3 است كه در آن c تعداد رده بندي هاست.

در مورد مثال طول مو دو رده بندي وجود دارد (c=2). دو نمونه هم وجود دارند كه به صورت متقابلاً مستقل بوده به گونه اي كه يك دانشجو نمي تواند به صورت همزمان در دو رده باشد. تصور كنيد كه بخواهيم تعداد 100 دانشجوي زن (N=100) را بررسي كنيم. در صورتيكه هيچگونه برتري اي از نظر طول مو وجود نداشته باشد انتظار مي رود كه نيمي از دانشجويان داراي موهاي بلند (با احتمال p1 = 0.5، كه گروه 1 گروه افراد با موي بلند است) و نيمي ديگر موهايشان كوتاه باشد (با احتمال p2 = 0.5، كه گروه 2 گروه افراد با موي كوتاه مي باشد). بنابراين زماني كه فرض صفر صحيح باشد انتظار داريم كه Np1 دانشجو 100 X 0.5=50 موهاي بلند و Np2 نفر (مشابه قبل 50 نفر) موهاي كوتاه داشته باشند. آيا تعداد 62 و 38 به طور معني داري با 50 متفاوت است و مي توان انتظار داشت هر گروه از فرض صفر پيروي كند؟

اينجاست كه χ^2 وارد مي شود. فرمولي كه در ادامه مي آيد توزيع χ^2 را زماني كه فرض صفر صحيح باشد بيان مي كند.

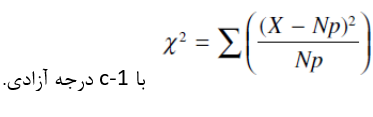
كه x فراواني مشاهده شده و Np فراواني مورد انتظار تحت صحيح بودن فرض صفر است.

اگرچه اين توزيع دقيق χ^2 نيست اما تا زماني كه بدانيم Np حداقل 5 است تقريبي مناسب است، بدين معني كه تحت فرض صفر فراواني مورد انتظار هر رده مي بايست حداقل 5 باشد. اين فرمول در واقع مقدمات رسيدن به توزيعي جهت مقايسه مقادير واقعي به منظور بررسي معني داري تفاضل ميان فراواني ها و مقادير مورد انتظار را فراهم مي كند.

در رابطه با آزمايش طول موي دو رده وجود دارد و مقدار χ^2 با استفاده از فرمول جديد به صورت زير محاسبه مي شود.

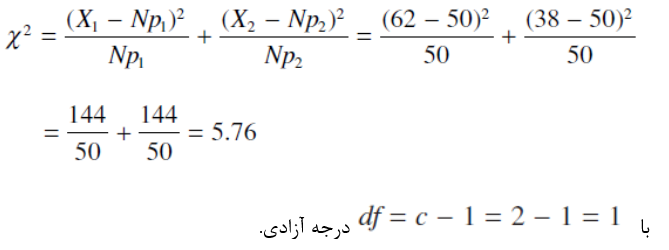
چنانچه جدول توزيع χ^2 مورد بررسي قرار داده شود (جدول A.7 ضميمه)، مقدار بحراني برابر 3.84= χ^2  با df=1 و p = 0.05. چون مقدار آماره ي محاسبه شده بزرگتر از مقدار بدست آمده از جدول است نتيجه مي شود كه دانشجويان دختر با موي بلند در محيط دانشگاه برتري معني داري دارند.

حالت معمولتر براي بيان فرمول ذكر شده براي χ^2 بدين صورت تغيير مي كند: X به عنوان فراواني مشاهده با (O) جايگزين شده و Np به عنوان فراواني مورد انتظار با (E)جابجا شده و در نهايت فرمول χ^2 كه در عمل مورد استفاده قرار مي گيرد عبارت است از:

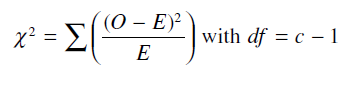
كاي اسكور (χ^2 ) به عنوان آزمون “نيكويي برازش” (goodness of fit)

در بسياري از موارد علاقه مند به بررسي معني دار بودن يا نبودن تفاوت فراواني هاي مشاهده شده با فراواني هاي مورد انتظار هستيم. معمولاً فراواني هاي مورد انتظار تحت درست بودن فرض صفر محاسبه مي شوند اما در حقيقت مجبور به اين كار نبوده و مي توان فراواني هاي مشاهده شده را هر كدام از فراواني هاي مورد انتظار كه علاقه مند هستيم مقايسه كنيم. به اين دليل است كه اين آزمون، “آزمون نيكويي برازش” ناميده مي شود و بر اين اساس مي توان تصميم گرفت كه آيا مجموعه اي از فراواني هاي مشاهده شده برازش مناسبي براي مجموعه خاصي از فراواني هاي مورد انتظار هستند يا نه.

مثال كاربردي

آزمايشگري مي خواهد بررسي كند كه آيا تفاوتي در برتري خودروها بر حسب رنگ آنها وجود دارد يا نه. براي اين كار به صد نفر شركت كننده تصاوير چهار خودروي يكسان كه فقط در رنگ متفاوت بودند جهت بيان برتري و اولويت آنها داده شد. رنگهاي خودروها عبارت بودند از قرمز، آبي، مشكي و سفيد.

در صورتيكه هيچگونه اولويتي وجود نداشته باشد انتظار مي رود كه هر كدام از رنگها به ميزان يكسان انتخاب شده و در نتيجه احتمال تعلق گرفته به هر كدام از رده ها تحت صحيح بودن فرض صفر برابر با 1/4 يا p = 0.25 باشد. با مقدار كل 100 (N)، انتظار مي رود فراواني تعلق گرفته به هر كدام از رده ها برابر Np از اين مقدار كل يعني 100 X 0.25، برابر با 25 باشد. بعد از انجام آزمايش محقق دريافت كه 48 نفر از شركت كنندگان خودروي قرمز، 15 نفر آبي، 10 نفر مشكي و 27 نفر سفيد را برگزيده اند. آيا تفاوت معني داري ميان اين فراواني هاي مشاهده شده و فراواني هاي مورد انتظار وجود دارد؟

جهت محاسبه ي χ^2 فراواني هاي مشاهده شده را با فراواني هاي مورد انتظار مقايسه مي كنيم.

آزمون “نيكويي برازش” در از توزيع نرمال

در بسياري موارد فراواني هاي مشاهده شده را با فراواني هايي كه تحت فرض صفر بدست مي آيند مقايسه مي كنيم اما موردي خاص وجود دارد كه در آن ممکن است مجموعه ی دیگری از فراوانی های مورد انتظار در نظر گرفته شوند. اغلب زماني كه می خواهیم فرضیاتی در زمینه نرمال بودن نمونه و يا نمونه های بدست آمده از یک جامعه انجام دهیم بعضی آزمونهاي پارامتري در نظر گرفته مي شود؛ که آزمون نيكويي برازش χ^2  آزمونی است که جهت بررسی استفاده می شود.

دويست نفر جهت بررسي هماهنگي چشم و دست در فعاليت هاي پيچيده آزمون شدند و تعداد خطاي ناشي از هر فرد اندازه گيري شد. نمرات در محدوده ي 22 تا 69 بودند. ميانگين نمونه برابر با X¯=46.86 و انحراف استاندارد آن برابر s=6 بدست آمد. آيا تفاوت معني داري ميان اين نمونه با توزيع نرمال وجود دارد؟

ابتدا جهت اتخاذ تصميم بايد رده ها انتخاب شوند. هر چه تعداد رده ها بيشتر باشد آزمون دقيق تر خواهد بود و در آن صورت نمرات اختصاص يافته به هر رده كمتر خواهد شد. با دامنه ي 22 تا 69 رده هاي با فاصله ي 5 ساخته شده كه تعداد آنها 10 تا مي شود كه در ستون اول جدول زير نمايش داده شده اند. كران هاي رده ها روي 0.5 تنظيم شده اند كه در واقع مقدار نيم كوچكتري احتمال تفاوت ميان دو نمره است. (كمترين تفاضل ممكن بين نمرات با خطاي يك برابر 1 است.) پس از انجام اين كار  هيچ دو رده اي همپوشاني نخواهند داشت. چنانچه مقدار 25 به عنوان كران يك رده در نظر گرفته شود در آن صورت نمره اي با مقدار 25 به هر دو رده ي 20–25 و 25–30 تعلق خواهد داشت، اما با رده ي 25.5 اين مقدار فقط به رده ي 20.5–25.5 تعلق خواهد داشت. اين بدين معني است كه در حاليكه همه رده ها پوشش داده مي شوند، فاصله ي خيلي زيادي ميان آنها وجود ندارد. مرحله ي بعدي اختصاص دادن 200 نمره به رده هاي خودشان است؛ كه اين فراواني هاي مشاهده شده در ستون دوم جدول نمايش داده شده اند.

اكنون نياز است كه روي فراواني هاي مورد انتظار محاسباتي صورت پذيرد. جهت انجام اين كار كران هاي رده ها را با استفاده از فرمول z به نمره ي z تبديل مي كنيم. متاسفانه ميانگين و انحراف معيار جمعيت جهت محاسبه ي نمره ي z وجود نداشته و لاجرم از مقادير نمونه اي آن يعني X¯و s.

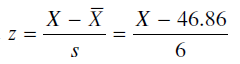برآورد شده

در اولين رده نمرات 20.5 و 25.5 به مقادير -4.39 و -3.56 تبديل مي شوند. اين كار براي تمام رده ها انجام مي شود. نتايج در ستون سوم جدول نشان داده شده اند.

در صورتيكه مقادير بدست آمده را با جدول توزيع نرمال استاندارد (جدول A.1 ضميمه) مقايسه كنيم، احتمال هاي متناسب با هر رده بدست خواهند آمد. اين احتمال ها در ستون چهارم جدول آمده اند. (به ياد آوريد احتمال تعلق گرفته به نمره ي z كوچكتر از -4 آنقدر ناچيز است كه برابر با صفر در نظر گرفته مي شود.) آنچه كه تفاوت احتمال بين كران هاي يك رده به ما مي گويد برابر با احتمال يافتن نمره اي در اين گروه است زماني كه توزيع جمعيت نرمال باشد. اين احتمال ها در ستون پنجم آمده اند. ( با توجه به آنكه در اطراف ميانگين هم نمره ي z مثبت و هم منفي وجود دارد، براي سادگي مي توان طرف منفي را در نظر گرفته و براي طرف ديگر مقدار 0.5 به مقدار بدست آمده اضافه شود )

مقادير فراواني هاي مورد انتظار با ضرب كردن احتمال هاي بدست آمده ي هر رده با فرض نرمال بودن توزيع احتمال ها (p) در تعداد كل شركت كنندگان (N = 200) براي هر رده بدست مي آيند كه در ستون ششم جدول نشان داده شده اند.

عناوين ستون به ترتيب از سمت راست:

X^2، فراواني هاي مورد انتظار ، تفاضل احتمال ها، احتمال، نمره ي z ، فراواني هاي مشاهده شده ، كران رده

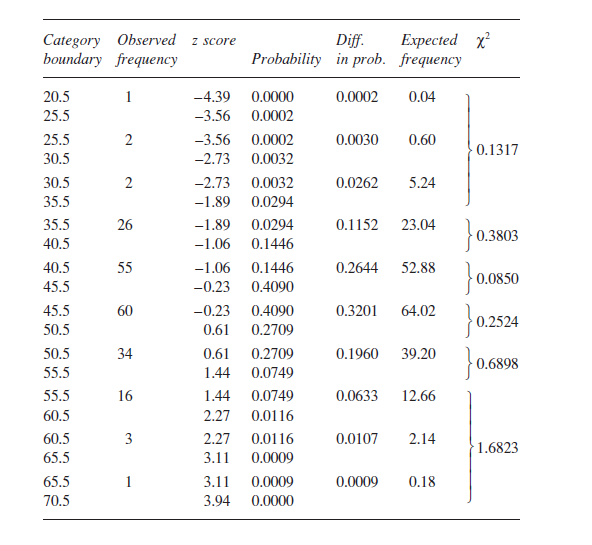
اكنون مي توان به محاسبه ي χ^2 پرداخت، گرچه هنوز رده هايي با فراواني كمتر از 5 وجود دارد و باعث مي شود آزمون مورد نظر از اعتبار ساقط شود. تركيب كردن رده ها كاري است كه در اين حالت انجام مي شود. اگر سه رده ي اول را با هم تركيب كرده و يك رده ي جديد ساخته شود و همين كار براي سه رده ي آخر نيز انجام شود در آن صورت روي هم رفته شش رده خواهيم داشت كه  در تمامي آنها فراواني هاي مورد انتظار بيشتر از 5 خواهد شد. فراواني هاي مشاهده شده در رده ي جديد 20.5–40.5 برابر با 5 و فراواني هاي مورد انتظار آن 5.88 است. ديگر رده ي جديد 55.5–70.5 فراواني هاي مشاهده شده اي برابر با 20 را به خود اختصاص  داده و فراواني هاي مورد انتظار براي آن 14.98 است. سرانجام:

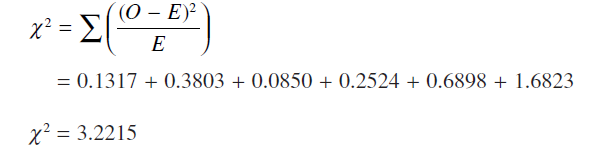
درجه ي آزادي يك واحد از تعداد رده ها كمتر و برابر با 6-1=5 مي شود. از آنجاييكه در اين مثال ميانگين و انحراف معيار جمعيت نامعلوم بودند از مقادير نمونه اي جهت برآورد كردن آنها استفاده شد. چون به ازاي هر بار برآورد كردن يك درجه آزادي مصرف مي شود در نهايت 3 درجه آزادي خواهيم داشت. با استفاده از جدول مقدار χ^2 با مقادير df = 3, p = 0.05 برابر با 7.82 خواهد بود. مشاهده مي شود كه مقدار آماره ي محاسبه شده از مقدار جدول كوچكتر است و بنابراين تفاوت معني داري ميان توزيع نمرات مثال ذكر شده با توزيع نرمال وجود ندارد.

آزمون استقلال كاي اسكور (χ^2 )

آزمون استقلال χ^2 مشابه با همان آزمون نيكويي برازش عمل كرده و فراواني هاي مشاهده شده را با فراواني هاي مورد انتظار مقايسه مي كند با اين تفاوت كه در آزمون استقلال براي بررسي متفاوت بودن فراواني ها از يكديگر (بررسي استقلال) دو يا تعداد بيشتري از جملات فراواني با هم مقايسه مي شوند. در مورد مثال افراد محافظه كار و ليبرال در ارتباط با وضع قانون مالياتي جديد، مي توان بررسي كرد كه آيا تفاوتي در فراواني هاي موافق و مخالف زماني كه بخواهيم افراد محافظه كار را با ليبرال ها مقايسه كنيم وجود دارد يا نه، كه اين كار با استفاده از آزمون χ^2 انجام مي شود.

 مثال كاربردی

محققي مي خواهد آزمون كند كه آيا تفاوتي ميان افراد محافظه كار و ليبرال در ارتباط با قانون مالياتي جديدي وجود دارد يا نه. در يك بررسي تعداد 120 نفر به عنوان افراد محافظه كار و 80 نفر ليبرال شناسايي مي شوند. آنچه كه در ادامه ي تحقيق لازم است دانسته شود تعداد افراد موافق، مخالف و ممتنع (افرادي كه هيچ نظري ندارند) در رابطه با وضع اين قانون مالياتي جديد است. نتيجه كار يعني مقادير مشاهده شده در جدول زير نمايش داده شده اند.

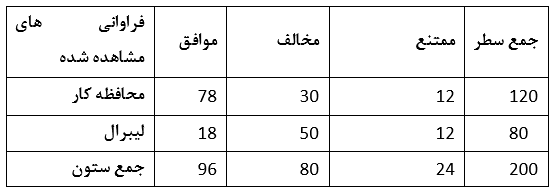
بايد توجه داشت كه با تعداد متفاوت افراد محافظه كار و ليبرال حتي تحت فرض صفر انتظار نمي رود که فراوانی های رده های مختلف یکسان باشد. از آنجاييكه تعداد افراد محافظه كار بيشتر از ليبرال ها است، اگرچه تعداد افراد با رأي ممتنع در هر دو گروه 12 نفر است اما در گروه محافظه كاران اين افراد از مقدار كل درصدي برابر با 12/120 يا 10 درصد را به خود اختصاص داده اند درحاليكه اين درصد براي گروه ليبرال ها برابر با 12/80 يا 15 درصد است؛ بدين معني كه در مقايسه ليبرال ها در مقايسه با محافظه كاران بيشتر پاسخ ممتنع مي دهند. انتظار مي رود زماني كه هيچگونه تفاوتي ميان دو گروه بر حسب پاسخ داده شده وجود نداشته باشد، درصد هاي بدست آمده در دو رده نزديك هم باشد. مقادير مورد انتظار تحت درست بودن فرض صفر با استفاده از فرمول زير محاسبه مي شوند.
ستون جمع X سطر جمع
————–= مقدار مورد انتظار هر سلول
جمع کل
به هر رده يك سلول تعلق مي گيرد و در حالت كلي شش سلول c 6 وجود دارد. ابتدا به عنوان مثال روي اولين سلول (افراد محافظه كار موافق) كار مي كنيم. در صورتيكه هيچگونه تفاوتي ميان دو گروه سياسي بر حسب درصد پاسخ “افراد موافق” وجود نداشته باشد، در آن صورت مي بايست از تعداد كل 96 نفري كه پاسخ موافق داده اند متناسب با تعداد كل هر كدام از دو رده هاي محافظه كاران و ليبرالها در اين دو رده جاي گيرند. بنابراين در صورتيكه تفاوتي ميان گروه ها وجود نداشته باشد انتظار مي رود از 96 نفر با پاسخ “موافق”، تعداد افرادي كه به روش زير محاسبه مي شوند به گروه محافظه كاران تعلق داشته باشند:

جهت اتخاذ تصميم مبني بر معني دار بودن بايد مقدار آماره ي بدست آمده را با توزيع χ^2 مقايسه كرد. در اين قسمت بايد دقت شود كه در اين حالت ديگر درجه ي آزادي برابر با تعداد رده ها منهاي يك يعني c-1نخواهد بود. زيرا در اين بخش مي خواهيم سطرها (دو گروه سياسي) را در مقابل نتايج بدست آمده از ستونها (عقايد مختلف) مقايسه كنيم و در حقيقت اين تفاوت بين دو روش نيكويي برازش و آزمون استقلال است. در اين بخش 2 سطر، R = 2 و 3 ستون C = 3 وجود دارد و در نهايت درجه ي آزادي براي آزمون استقلال به صورت زير محاسبه مي شود:

df = (R – 1)(C – 1)

در مورد مثال ذكر شده خواهيم داشت df = (2 – 1)(3 – 1) = 2 . با توجه به جدول داريمX^2=9.21, df=2, p=0.01  . چون مقدار آماره ي محاسبه شده بزرگتر از مقدار جدول است در سطح معني داري p = 0.01 فرض صفر رد شده و تفاوت معني داري ميان پاسخ هاي بدست آمده از دو گروه محافظه كار و ليبرال به وضع قانون مالياتي وجود دارد.

جهت بهبود χ^2 مي بايست از بزرگتر بودن فراواني هاي مورد انتظار از 5 اطمينان حاصل كرد. در مورد اين مثال مسئله ي خاصي ايجاد نشد. اما اگر مثلا تعداد قليلي رأي “ممتنع” داشته باشند و فراواني هاي مورد انتظار اين رده كمتر از 5 باشند بايد رده ي “ممتنع” را حذف كرده و جهت يك آزمون معتبر فقط افراد “موافق” و “مخالف” مقايسه شوند و يا به عنوان راهي ديگر جهت نايل شدن به فراواني هاي بزرگتر داده هاي بيشتري گردآوري شوند.

توزيع χ^2

مربع يك مقدار و يا مجموع مربعات در χ^2 باعث مي شود كه اين مقدار هميشه بزرگتر از صفر باشد. همچنين شكل توزيع با تغيير درجه ي آزادي، تغيير مي كند. تحت فرض صفر انتظار مي رود كه مجموع مربعات حول صفر پراكنده شده باشند اما تغييرات تصادفي بدين معني است كه تحت فرض صفر هميشه

اين مقادير دقيقا برابر با صفر نيستند.  اگر تعدادي مقادير مثبت كه هر كدام فقط مقدار جزئي از صفر بزرگتر باشند به اين مجموع مربعات اضافه شود اين مقدار به نسبت تعدادي كه به آن اضافه شده، افزايش نسبي تدريجي خواهد داشت. در اين حال به نسبت مجموع مربعاتي كه داريم درجه ي آزادي بزرگي ايجاد مي شود.

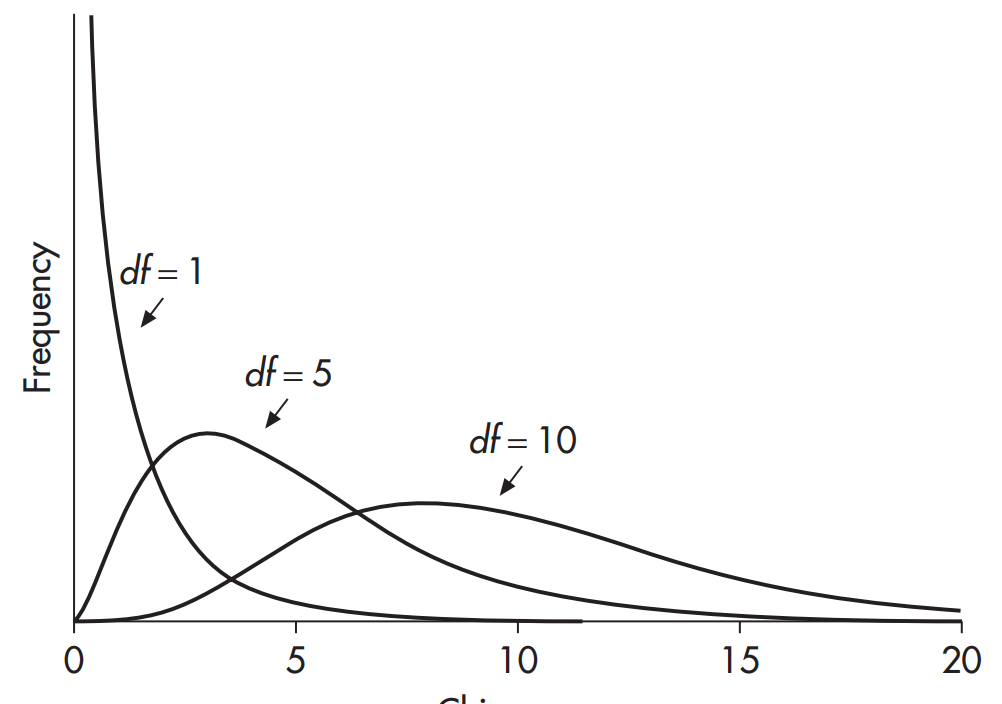
زماني كه df=1 انتظار مي رود تحت فرض صفر بيشتر حاصل شده به صفر نزديك بوده و تفاوت ميان مقادير مشاهده شده و مورد انتظار كم باشد. (شكل 19.1 را نگاه كنيد). در صورتيكه مقادير موجود در توزيع نرمال استاندار به توان دو برسند نمودار حاصله مشابه با اين نمودار خواهد شد. اگر درجه ي آزادي افزايش يابد بدين معني است كه مجموعه اي از مقادير مستقل χ^2 كه درجه ي آزادي هر كدام يك است با مجموع مربعات موجود جمع شده اند. براي مثال فرض كنيد df =5، در آن صورت پنج جمله ي مستقل χ^2 وجود خواهد داشت. اگرچه هر كدام از جملات χ^2 نزديك صفر هستند، زماني كه تمامي جملات با يكديگر جمع شوند مجموع آنها به اندازه اي خواهد بود كه شكل توزيع را تا حدودي تغيير مي دهد(شكل 19.1 را مشاهده كنيد). همچنانكه درجه ي آزادي افزايش مي يابد ميانگين توزيع به سمت جلو حركت كرده و شكل توزيع را تغيير مي دهد به گونه اي كه براي درجات آزادي كوچك توزيع بسيار نامتقارن بوده ولي با افزايش درجه ي آزادي شكل توزيع متقارن تر مي شود. (df= 10 را در شكل 19.1 مشاهده كنيد). براي درجات آزادي 30 و بيشتر مي توان توزيع را با نرمال تقريب زد. در نتيجه معمولا در df=30 و بالاتر مي توان به جاي توزيع χ^2 از توزيع نرمال استفاده كرد (جدول A.7 ضميمه).

فرضيات آزمون χ^2

به منظور مقايسه ي آماره ي محاسبه شده ي χ^2 با مقدار مناسب جدول مي بايست زماني كه آزمون χ^2 انجام مي شود فرضيات خاصي برقرار باشد.

همانند بسیاری از توزیع ها مي بايست نمونه ي انتخابي به صورت تصادفي از از جمعيت انتخاب شده باشد و در غير اينصورت اريبي نمونه نتايج را تحت تأثير خود قرار مي دهد. در توزيع χ^2 متقابلاً مستقل بودن رده ها امري ضروريست. بايد توجه داشت كه يك آزمودني در ساختن فراواني بيش از يك سلول نمي تواند شركت داشته باشد.

توزيع مربع كاي توزيعي پيوسته است، بدين معني كه هيچ پرشي در آن وجود نداشته و منحني اي پيوسته است. در حاليكه مقادير محاسبه شده در آزمون χ^2  مقياسي پيوسته نداشته و به صورت مقاديري گسسته هستند و دليل اين امر هم تغيير كردن فراواني هاي مشاهده شده در واحدهايي گسسته است، به عنوان مثال فراواني هاي 10 يا 11 قابل مشاهده هستند اما 10.4 يا 10.6 وجود ندارند. با وجود درجات آزادي بزرگتر از 1 و همچنين فراواني هاي مورد انتظار حداقل 5 (و ترجيحاً 10)، تفاوت بسيار كوچكي ميان آماره و توزيع دقيق نمونه گيري ايجاده كرده كه مشكلي ايجاد نمي كند. در واقع اين دليل گرايش به سمت سلول هايي با فراواني بزرگ است. به عنوان مثال تفاوت بين 100 و 101 كم و برابر با 1/100 يا يك درصد از فراواني اصلي است. در حاليكه 5 يا 6 واحد تفاوتي برابر با 1/5 يا 20 درصد ايجاد كرده كه مي توان گفت يك جهش بزرگ است. همچنين به دليل آنكه در تقسيم بندي واحد ها به نوعي دچار محدوديت هستيم (نمي توان واحدي كوچكتر از يك داشت)، در صورت كوچك بودن فراواني سلول ها هر گونه تفاوتي ميان فراواني هاي مشاهده شده و مورد انتظار (حتي به كوچكي 1) بزرگ جلوه مي دهد كه در اين حال مقدار آماره χ^2 به سمت بزرگ شدن ميل مي كند (و احتمال رخ دادن خطاي نوع اول وجود دارد).

جهت جبران اين مشكل زماني كه df = 1  از تصحيح ناپيوستگي ييتس (). جهت تعديل فرمول χ^2 به روش زير عمل مي شود.

تصحيح شده

خطوط دو طرف O – E به معناي قدر مطلق است، بدين معني كه اگر تفاضل مقداري منفي باشد از علامت منفي آن چشم پوشي كرده و به عنوان يك مقدار مثبت با آن رفتار مي شود. بنابراين مقدار χ^2 هر سلول قبل از اينكه به توان دو برسد از 0.5 كم مي شود كه منجر به يك مقدار χ^2 ي كوچكتري مي شود و ريسك رخ دادن خطاي نوع اول را كم مي كند. در هر صورت تصحيح ييتس جبراني براي ناپيوستگي ها بوده كه حتي ممكن است به نوعي منجر به تصميمات محافظه كارانه تري شود. اين مسئله تنها زماني كه فرض معني داري پس از تصحيح پيوستگي از معني داري ساقط شود مطرح مي شود. در اين موارد مي بايست با وجود داشتن چنين داده هايي بيشتر توجه داشت. در هر صورت در مواردي كه به نوعي شك و شبهه وجود داشته باشد (نزديك به معني داري اما نه كاملاً معني دار) مي بايست ابهامات موجود را با افزايش حجم نمونه و يا طرح سؤالات بيشتر ترفيع كرد.

جزئيات چگونگي محاسبه ي آماره ي كاي دو با استفاده از پكيج آماري SPSS  را مي توان در فصل 14 هينتون و ديگران (2004).

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا

برای دسترسی به جدیدترین مقالات آموزشی آمار کلیک کنید.