مقدمه ای بر مدل خطی عام- بخش 1

آخرین به‌روزرسانی: 24 دی 1401

در مقاله قبلی به بررسی كامپيوتر و تحليل های پيچيده پرداختیم. در این فصل به آموزش مدل خطی عام، در ادامه سری مقالات آموزشی آمار به زبان ساده می پردازیم.

 

بسیار شگفت انگیز است اگر بدانید اصول اساسی آماری مانند آزمون تی، آنالیز واریانس، همبستگی و رگرسیون و همچنین آزمون های چند متغیره که در فصل های قبل بررسی شد و همچنین مباحثی مشابه، همگی مثالهایی از مدل خطی عام (general linear model) هستند. به نظر می رسد این آزمون ها اهدافی متفاوت و محاسباتی غیرمشابه داشته باشند و در نتیجه آماره های متفاوتی را مانند t، F و یا r سبب شوند که در ظاهر به نظر می رسد کاملاً با یکدیگر فرق داشته باشند. به هر حال با توجه به انتظارات متفاوتی که از داده ها داریم از چنین آزمونهایی استفاده خواهیم کرد؛ همچنین ممکن است فرضیات تحت آزمون در مواردی بسیار شبیه به یکدیگر باشند.

یافتن کلیه ی مواردی که به آن علاقه مند هستید امکانپذیر است اما در حالت کلی ممکن است ارتباط چندانی به شما نداشته باشد؛ ما هم می توانیم از آمار استفاده کنیم بدون اینکه اطلاعی دقیق از مدل خطی عام بدانیم، مشابه با فردی که بدون اینکه از چگونگی کار کردن موتور خودرو اطلاعی داشته باشد از رانندگی با آن لذت می برد. در صورتیکه خودروی شما خراب شود و اطلاعاتی از نحوه ی عملکرد موتور آن داشته باشید قادر خواهید بود آن را مجدد راه اندازی کنید (خصوصاً اگر مشکل آن یک انسداد ساده و یا کمبود سوخت باشد) درغیر این صورت اگر هیچگونه اطلاعی نداشته باشید می بایست منتظر خودروی امداد بمانید. به طور مشابه درک عمومی از مدل خطی عام شرایطی را فراهم می کند که آگاهی از آنچه در یک آزمون اتفاق می افتد و اینکه آیا داده ها مناسب با آن آزمون می باشند یا خیر از نتایج آن است. عدم آگاهی از اساس مدل خطی عام منجر به درک نادرستی از فرضیات آزمونهای آماری می شود و در آن صورت حتی متوجه بعضی از فرضیاتی که به نادرستی ایجاد کرده ایم، نخواهیم شد.

مدلها

به صورت کلی زمانی که از مدل (منظور مدل، مد روز نیست) صحبت می شود، آنچه که به ذهن می آید چیزی مانند مدل یک خودرو و یا مدل برج ایفل است. توجه داشته باشید که این مدلها بازنمایی از اشیایی هستند که مدلسازی می شوند. بعضی از آنها مانند مدل مقیاس جزئی برج ایفل بازنمایی های بسیار خوبی هستند اما برخی دیگر مانند مدلهای صورتی کرکی از برج ایفل که می توان آنها را از مغازه های سوغاتی در پاریس تهیه کرد خیلی مدلهای مناسب و جالبی نیستند. اما در حالت کل حتی همان مدلهای ضعیف کرکی برج ایفل نیز می بایست تا حدودی شباهت به نمونه ی اصلی آن داشته باشند. بنابراین در بحث مدل به دنبال الگویی اساسی از چیزی هستیم که قصد مدلسازی آن را داریم.

شكل 23.1 جهان نما

یک مثال کلاسیک مدل، جهان نما است و مدلی از سیستم خورشیدی بوده که احتمالاً آن را در موزه ها و مجموعه ای از اشیاء عتیقه مشاهده کرده باشید. اولین نمونه ی آن در سال 1712توسط ساعت ساز معرف یعنی جان رولی برای چارلز بویل ساخته شد که نام آن هم از همین جا گرفته شده است. آنچه در شکل 23.1 مشاهده می کنید جهان نمایی است که در مؤسسه اسمیتسونیان (Smithsonian) واقع در واشنگتن دی سی بنا شده است.

جهت راه اندازی مدل باید دسته را گردانده به گونه ای که سیارات اطراف خورشید به چرخش درآیند. این مدل به سادگی قادر است طرحی ساده از چگونگی کارکردن سیستم خورشیدی را ارئه دهد و اینکه چگونه سیارات نسبت به یکدیگر حرکت می کنند و همچنین سال به چه معناست و اطلاعاتی مشابه با آن را ارائه می دهد. همچنانکه این مدل کمک قابل توجهی در یادگیری دارد ولی از جنبه های دیگر مدل ضعیفی به شمار می آید؛ زیرا مقیاس به کار برده شده برای اشیاء موجود در آن مناسب نیستند و خورشیدی که در مرکز آن است نیاز است بسیار بزرگتر باشد، همچنین در حالت واقعی سیارات حول خورشید در یک محور بیضی می چرخند نه دایره ای. این مدل قطعاً مدلی نیست که بتوانید به عنوان راهنمای فضانورد در فضا استفاده کنید.

با وجود این بشریت تا کنون با استفاده از فضاپیماها به ماه و سایر سیارات و مراکز فضایی سفر کرده است و لازمه ی آن وجود مدلهای خورشیدی است تا بتوان سفری موفقیت آمیز به آنها داشت. واضح است که چنین مدلهایی در مقایسه با مدل جهان نما به طور قابل توجهی پیچیده تر هستند اما تفاوتی که با آن دارند این است که دیگر این مدل ها در کارگاه و توسط یک ساعت ساز ساخته نشده اند و با پایه گذاری آنها بر اساس ریاضیات است و به جای اشیاء فیزیکی، فرمولهای ریاضی نوشته شده که در کامپیوتر ذخیره می شوند. در صورتیکه بخواهیم جایگاه سیارات مریخ و زهره را در طول شش ماه بدانیم به جای اینکه دسته ی جهان نما را چرخانده و موقعیت های جدید سیارات را بررسی کنیم، داده های زمان را به مدلهای ریاضی در کامپیوتر داده و جزئیات موقعیت های جدید پیش بینی شده (predicted) توسط مدل را بدست آوریم. در صورتیکه مدل مناسبی داشته باشیم، موقعیت های بدست آمده صحیح پیش بینی خواهند شد.

مدلها ویژگیهای مشابهی را جهت تلاش در ارائه روابط میان یک سیستم خاص به اشتراک می گذارند (مانند حرکت سیارات). در مواردی که دریابیم کارکردن سیستمی تصادفی نیست می توان در جستجوی مدلی به منظور نمایش الگوی مشاهدات بود.

از زمان های قدیم انسانها به بالا و پایین رفتن خورشید و همچنین تغییرات فصلی توجه داشته اند و همواره در تلاش بوده اند تا الگویی از آنچه مشاهده می کردند، بسازند. مدلهای ریاضی موجود جهت استفاده در به زمین نشستن فضاپیماها در سایر سیارات کاملاً مؤثر هستند اما کسی نمی داند شاید تا سیصد سال دیگر مشابه با آنچه که در ارتباط با جهان نما رخ داد، این اطلاعات هم برای انسانها در آینده کاملاً ساده و ابتدایی باشد.

مثالی از مدل خطی

زمانیکه داده ها جمع آوری می شوند خیلی علاقه مند به رخ دادن داده هایی خاص در زمانهای مشخص نیستیم و در عوض می خواهیم با استفاده از روابط موجود میان متغیرها در مجموعه ی داده ها به پیش بینی بپردازیم. روشی جهت انجام این کار ساختن فرضیه ی وجود رابطه میان متغیرها و پس از آن تلاش در مدلسازی آن رابطه است. پس از آن مشابه با جهان نما، در مورد مناسب بودن و یا نبودن مدل تصمیم گیری می شود.

یک نوع خاص از این مدل که جهت تجزیه و تحلیل آماری استفاده می شود مدل خطی نام دارد. چنانچه در فصل 20 مشاهده شد، در ساده ترین حالت و تنها با وجود رابطه ی میان دو متغیر مدل خطی به یک خط مستقیم تبدیل می شود و فرمول ریاضی خط مستقیم عبارت است از Y=a+bX، که متغیرها در آن X و Y هستند و a مقدار ثابت بوده (در واقع مقدار Y زمانی که X صفر باشد و نقطه ای است که محور Y را قطع می کند) و b شیب خط است.

تصور کنید به فردی بسته ای از کارتهای بازی می دهید و از او می خواهید با هر سرعتی که می تواند به مرتب کردن آنها (البته بدون اشتباه) در دو بخش بپردازد، بخش اول کارتهای قرمز و دیگری کارتهای سیاه. حین مرتب کردن بسته، زمان لازم برای انجام این کار اندازه گیری می شود. فرض کنید زمانی برابر با 20.8 صرف شود. بار دیگر کارتها را مخلوط کرده و از او بخواهید کارتها را در چهار دسته طبقه بندی کند. زمان صرف شده برابر با 31.2 ثانیه ثبت می شود. سرانجام از او بخواهید که بسته کارتها را به 8 دسته تقسیم کند: کارتهای با تعداد قلب کم (آس تا هفت)، کارتهای با تعداد قلب زیاد (8 تا پادشاه)، الماس کم، الماس بالا و غیره. اکنون این ارقام را روی نمودار رسم می کنیم (شکل 23.2).

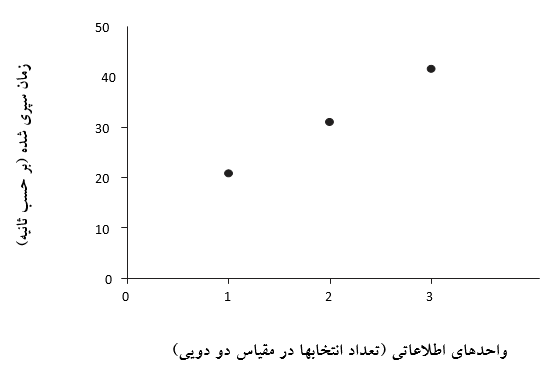
شکل 23.2- نمودار زمانهای سپری شده حین مرتب کردن کارتها

می بینید که محور X به جای “تعداد بخش” با “واحدهای اطلاعاتی” برچسب گذاری شده است. یک انتخاب تکی (شامل دو گزینه: به عنوان مثال روشن/خاموش یا قرمز/سیاه) شامل یک واحد اطلاعاتی (یک واحد دو دویی از اطلاعات یعنی bit) است. چهار گزینه شامل دو واحد اطلاعاتی (دو bit) و هشت گزینه شامل سه واحد اطلاعاتی (سه bit) است. دلیل اینکه ما از واحدهای اطلاعاتی به جای تعداد گزینه ها استفاده می کنیم این است که محققانی که برای اولین بار در اوایل دهه 1950 این مطالعه را انجام دادند، متوجه شدند که الگوی نتایج هنگام رسم نمودار به این روش یک خط مستقیم را دنبال می کند. آنها داده های قابل توجه تری را جمع آوری کردند که بسیار متنوع تر از مثال ذکر شده در بالا بود. مدل حاصل، بیانگر رابطه ای خطی بین میزان اطلاعات و سرعت پردازش است و محققانی که آن را یافتند را جاودانه کرده و از آن به عنوان قانون هیک-هیمن ( Hick–Hyman Law) یاد می شود.

در ارتباط با شرکت کنندگان فوق، می توانیم فرمول خط مستقیمی که از این سه نقطه عبور می کند را با قرار دادن سه نقطه در فرمول Y = a + bX و بدست آوردن “a” و “b” به صورت Y = 10.40 + 10.40X بنویسیم که بیان می کند:

(واحد اطلاعاتی × 10.40) + 10.40= زمان سپری شده

اکنون می توانیم از این مدل برای پیش بینی آنچه نمی دانیم استفاده کنیم. اگر فرد مجبور باشد بسته ها را بر اساس تعداد زیاد، میانی و کم تقسیم بندی کند (12 گزینه یا 3.585 واحد اطلاعاتی)، انتظار داریم که 10.40+ ((10.40 × 3.585) = 47.68 ثانیه طول بکشد).

مدل بندی داده ها

در اکثر شیوه های آماری فرض بر این است که یک مدل خطی الگوی رابطه بین متغیرها را نشان می دهد و بدون استفاده از این مدل قادر به استخراج تحلیل های آماری نیستیم. همانطور که دانشمندان فضایی برای فرود یک فضاپیما در مریخ به مدلهای خود نیاز دارند، ما نیز برای تصمیم گیری آماری به یک مدل نیاز داریم. در این مثال ما یک مورد پیچیده تر از سه نقطه در نظر گرفته شده در مثال مرتب سازی کارت های بالا را در نظر خواهیم گرفت و در این مثال جدید امتیازات ما به طور منظم در امتداد یک خط مستقیم قرار نمی گیرند.

محققی به رابطه بین سن کودک و دانش عمومی او علاقه مند است. برای داشتن استدلالی صحیح فرض می کنیم که به طور مقتضی محقق قادر به انتخاب یک مدرسه مناسب است و به طور تصادفی 6 کودک را از کلاسهای سه سال تحصیلی انتخاب می کند: کلاس 1 (تقریبا 8 ساله)، کلاس 2 (تقریبا 9 ساله) و کلاس 3 (تقریباً 10 ساله). به هر کودک آزمون دانش عمومی یکسان داده می شود و نمرات ثبت می شوند. نتایج به دست آمده در جدول زیر نشان داده شده است.

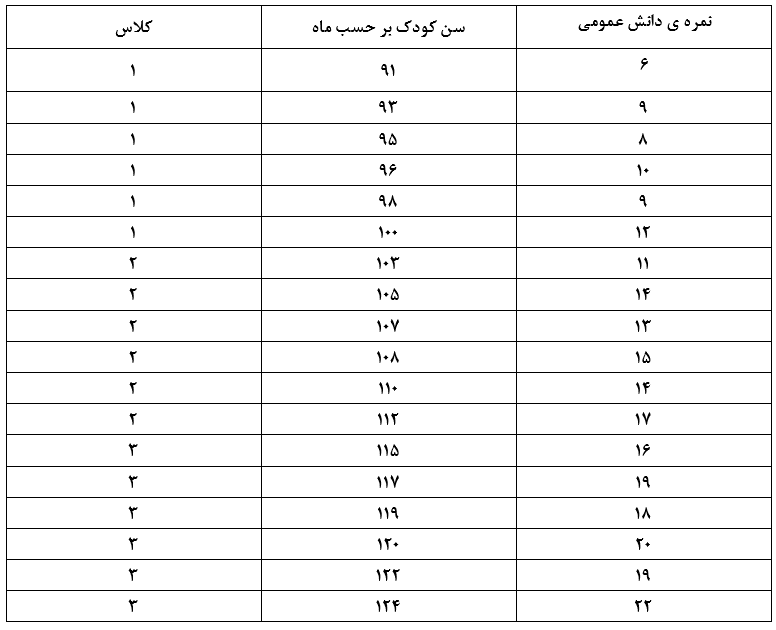
شكل 23.3. نمودار نمرات دانش عمومی کودکان براساس سن

آیا نتایج تصادفی است یا بین سن و نمره دانش عمومی رابطه منظمی وجود دارد؟ مطمئناً با توجه به اطلاعات موجود در جدول اقتباس می شود که با افزایش سن، نمرات بیشتر می شوند. این مسئله را با رسم نمودار نتایج بدست آمده می توان مشاهده نمود، همانطور که در شکل 23.3 نیز نشان داده شده است.

اکنون در مراحل ابتدایی با نگاهی به داده های موجود در نمودار این فکر به ذهن خطور می کند که برای چه به مدل نیاز داریم؟ می توان ادعا کرد که هر نقطه در نمودار نمایشی واقعی از سن و نمره کودک است. اما در حالت کلی این چیزی نیست که ما واقعاً می خواهیم بدانیم. در حقیقت هدف ما بدست آوردن اطلاعاتی بدین صورت نیست که مثلا جان پیترسون در روز پنجشنبه 8 سال و 4 ماه دارد و در آزمون دانش عمومی نمره 12 را کسب کرده است. آنچه واقعاً علاقه مندیم یاد بگیریم این است که آیا رابطه معنی داری بین سن و دانش عمومی وجود دارد یا خیر. در صورت وجود از این رابطه می توانیم در کودکانی که آزمایش را برای آنها انجام نداده ایم، برای پیش بینی اینکه چه سطح از دانش عمومی را می توان از رده های سنی مختلف انتظار داشته باشیم، پیش بینی کنیم. در نهایت می توانیم یافته های خود را به جمعیت بیشتری تعمیم دهیم.

چنانچه به دقت به داده ها نگاه کنیم، به نظر می رسد نمرات به صورت کم و بیش یک خط مستقیم را دنبال می کنند. توجه داشته باشید که همه آنها در یک باند باریک قرار دارند که از پایین سمت چپ به سمت راست بالا در شکل 23.3 قرار گرفته اند و هیچ نمره ای در سمت چپ بالا و یا سمت راست پایین قرار نگرفته است. بنابراین می توان پیشنهاد کرد که رابطه بین نمرات دانش عمومی و سن خطی است (در این حالت یک خط مستقیم) و مدل برازش داده شده به داده ها یک مدل خطی است. لذا اگر رابطه بین متغیرها واقعاً یک خط مستقیم است، پس آن خط باید جایی در وسط نقاط قرار بگیرد، مانند نمودار 23.4.

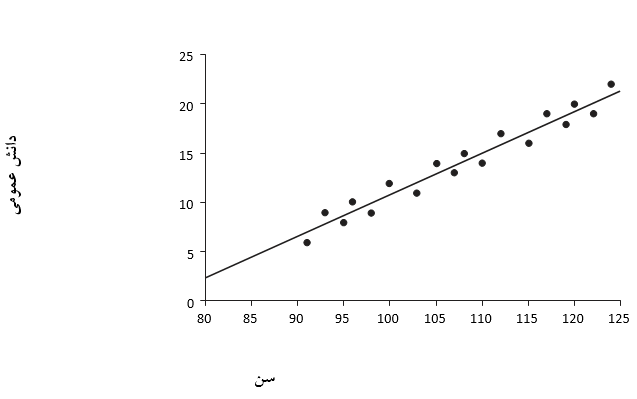
شكل 23.4. رابطه خطی پیشنهادی میان دانش عمومی و سن

اکنون در اینجا یک مشکل وجود دارد. در واقع هیچ یک از نقاط روی خط قرار ندارند! آیا این بدان معنی است که این خط مستقیم یک مدل ضعیف از رابطه بین نمرات دانش عمومی و سن است؟ نه لزوماً. نخست باید گفت که نقاط کاملاً نزدیک به خط به نظر می رسند (که مطمئناً نشان می دهد مدل چندان بد نیست). ثانیاً نکته دیگری که از این نمودار می توان استدلال کرد این است که ما در جهانی با وجود خطا و شانس زندگی می کنیم و می توان گفت این مسئله هم از آن مستثنی نیست. شاید یک کودک به دلیل سرماخوردگی عملکرد کمتری داشته باشد و دیگری به دلیل اینکه توانسته پاسخی را حدس بزند بهتر از حد معمول عمل کرده باشد. در زندگی روزمره عواملی وجود دارند که سبب بهم ریختگی موضعی آن می شوند و اینکه همیشه همه چیز به آن صورتی که ما انتظار داریم پیش نمی رود. شاید اگر آلودگی (یا خطاهای تصادفی) را برطرف کنیم، الگوی اصلی (در صورت وجود) پدیدار شود. من پیشنهاد می کنم که در یک جهان ایده آل تمام نقاط در امتداد خط قرار می گیرند. در این مثال، ممکن است به دلیل این خطاهای تصادفی که در هر فعالیت انسانی مانند روش تحقیق رخ می دهد، علیرغم تلاش ما برای کنترل، نمرات کاملاً روی خط قرار نگیرند (برای استدلال مرتبط به فصل 10 مراجعه کنید).

بنابراین می توان استدلال کرد که مدل واقعی برای تبیین رابطه بین نمرات دانش عمومی و سن یک خط مستقیم است و دلیل عدم انطباق کامل نمرات روی خط مستقیم به دلیل رخداد خطای تصادفی است. از این رو هر نمره مشاهده شده از نمره پیش بینی شده توسط مدل (“تغییر تبیین شده”) به علاوه یک خطای تصادفی (“تغییر تبیین نشده”) تشکیل شده است.

هر نقطه در شکل 23.5 نمره دانش عمومی یک کودک را نشان می دهد. توجه داشته باشید که نسبت قابل توجهی از نمره دانش عمومی را می توان توسط مدل (خط شیب دار) محاسبه کرد، زیرا نقاط کم و بیش روی خط قرار دارند، لذا میزان “خطا”ی نمرات – تفاوت بین نمره واقعی و پیش بینی شده توسط مدل – بسیار کوچک به نظر می رسد. میزان خطا با اتصال میله عمودی نقطه به خط نشان داده می شود.

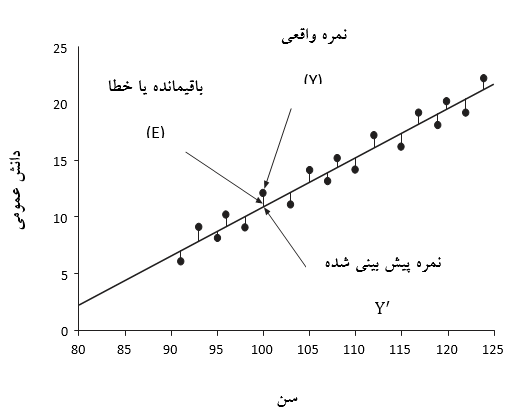
شکل 23.5. تفکیک نمرات بر اساس نمره پیش بینی شده و مقدار باقیمانده

اگر نمره دانش عمومی یک کودک را در نظر بگیریم، که من آن را Y می نامم، پس می توانیم بخش زیادی از آن نمره را با مدل خود تبیین کنیم (بدین معنی که یک نقطه از خط مستقیم که می توانیم نمره آن را پیش بینی کنیم) که می توان آن را قرار دهیم. اما، چون نمره در امتداد خط مستقیم قرار نمی گیرد، لذا Y برابر با نیست. در نتیجه استدلال می کنم که E، تفاوت بین Y و، به اصطلاح “خطا” است، زیرا من معتقدم که رخداد این امر به دلیل وجود خطای تصادفی است و با مدل من قابل تبیین نیست. اصطلاح دیگری که برای E بکار برده می شود باقیمانده است، زیرا هر یک از این مقادیر برابر است با مقدار باقیمانده نمره دانش عمومی پس از اینکه مقدار توضیح داده شده توسط مدل را از آن کم کنیم. بنابراین برای هر نمره:

باقیمانده (E)+ نمره پیش بینی شده ()= نمره واقعی (Y)

مدل: معادله رگرسیونی

در بخش قبل خطی مستقیم به عنوان مدلی برای تبیین رابطه بین سن و نمره دانش عمومی پیش بینی شد. حال مسئله این است: کدام خط؟ می توان جواب این سؤال را با نگاه کردن به شکل 23.6 پاسخ داد.

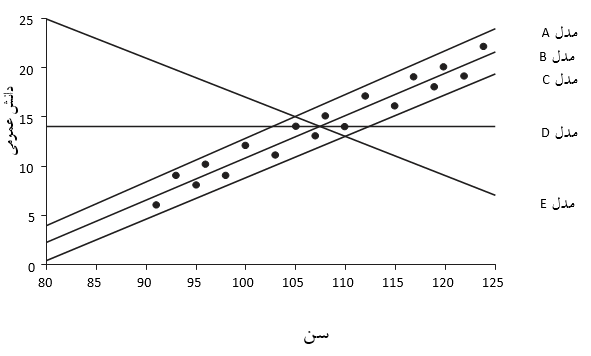
شکل 23.6- مدل های خطی متفاوت

مدل C مشخصاً مدل خوبی نیست زیرا خط کاملاً پایین تر از نقاط واقعی داده است. این مسئله را از طریق روابط ریاضی نیز می توان دریافت، زیرا باقیمانده ها همه مقادیر مثبت و جمع آنها عدد مثبت زیادی خواهد بود. به دلیلی مشابه مدل A نیز با داده ها خیلی مطابقت ندارد، زیرا باز هم باقیمانده ها یک مقدار منفی بزرگ را نتیجه می دهند. مدل B از آنجایی که در مابین داده ها قرار گرفته است، نه تنها بهترین مدل به نظر می رسد بلکه مقادیر باقیمانده کوچکتری نیز نسبت به مدل های A و C دارد. در این حالت برخی از باقی مانده ها مثبت (نقطه بالای خط قرار دارد) و برخی منفی (نقطه زیر خط قرار دارد)، لذا پس از جمع نهایی با یکدیگر حذف و خنثی می شوند. بنابراین بهترین مدل قابل برازش خطی مستقیم خواهد بود که در آن حاصل جمع باقیمانده ها صفر می شوند.

روش دیگری برای برازش مدل استفاده از این خاصیت است که میانگین باقیمانده ها در بهترین خط برازش داده شده برابر با صفر است. این مسئله منطقی به نظر می رسد زیرا در این حالت، مقدار “متوسط” خطا صفر خواهد بود. با نگاهی به مدلهای A و C در نمودار بالا می توان دریافت که باقیمانده ها میانگینی برابر با صفر نخواهند داشت، چنانچه پیشتر ذکر شد این مدل ها برای برازش به داده ها مناسب نیستند. در حقیقت مقادیر میانگین باقیمانده های آنها بیان کننده ی میزان انحراف خط مورد نظر نسبت به بهترین خطی است که می تواند به داده ها برازش داده شود. از سوی دیگر مقدار میانگین صفر نشان می دهد که خط برازش داده شده کاملاً از میانگین داده های مربوط به سن و دانش عمومی عبور می کند.

مسئله ناخوشایندی که وجود دارد این است که اگر به مدل های B ،D و E نگاه کنیم، در هر سه مورد متوجه می شویم که خط برازش داده شده از میانگین های مقادیر سن و دانش عمومی عبور کرده است (ماه 107.5 و نمره 14). در هر سه مدل حاصل جمع باقیمانده ها برابر با صفر می شود (در صورت تمایل می توانید آنها را حل کنید) و میانگین باقیمانده های آنها نیز صفر خواهد بود. با این حال، برای دیدن اینکه هر دو مدل D و E با داده ها بسیار ضعیف هستند، نیاز به مشاهده زیادی ندارد. تفاوت مدل B با مدل های D و E این است که مدل B مدلی با کمترین مقادیر باقیمانده ای است.

اکنون باید معادله خط با کوچکترین مقادیر باقیمانده را پیدا کنیم به طوریکه حاصل جمع باقیمانده ها صفر شود (مدل B). این کار را با در نظر گرفتن رگرسیون سن بر روی نمره های دانش عمومی (که در فصل 20 شرح داده شده است) انجام می دهیم، که ماحصل آن مدلی با “بهترین برازش” به داده ها است. روش رگرسیون خطی بر اساس فرض خطی بودن مدل بنا شده است و بر پایه تجزیه و تحلیلهای فرض مدل خطی استوار است. در واقع این روش، مدل خطی ای را پیدا می کند که در آن باقیمانده ها را به حداقل می رساند و از این رو بیشترین تغییرات داده ها توسط مدل خطی، نسبت به سایر مدلهای خطی که می توان در نظر گرفت، تبیین می شود.

فرض کنید که نمرات دانش عمومی مشاهده شده (Y) ترکیبی از مدل خطی (خط رگرسیون ) به علاوه خطاها یا باقیمانده ها (E) هستند:

Y = Y′+ E

همانطور که میدانید فرمول خط مستقیم به صورت Y ′ = a + bX است (که در آن نمره دانش عمومی پیش بینی شده و X سن کودک است)، بنابراین:

Y = a + bX + E

بر این اساس می توان فرمولی برای E به صورت زیر ارائه داد:

E = Y − a − bX

اکنون حاصل جمع باقیمانده ها به صورت

از نتیجه این تجزیه و تحلیل فرمول زیر حاصل می شود که بهترین خط مستقیم را به داده ها برازش می دهد:

Y′=−31.77 + 0.43X( برای دقت بیشتر,

a =−31.7665 and b = 0.4257)

در واقع با استفاده از این فرمول به طریق زیر می توان پیش بینی انجام داد:

دانش عمومی =−31.77 + (0.43 × سن)

اکنون می توانیم با قرار دادن مقادیر سن در معادله مذکور، نمرات دانش عمومی پیش بینی شده را بدست آوریم و سپس مقادیر باقیمانده را (با داشتن مقادیر واقعی نمرات دانش عمومی) محاسبه کنیم. این مقادیر در جدول زیر نمایش داده شده اند.

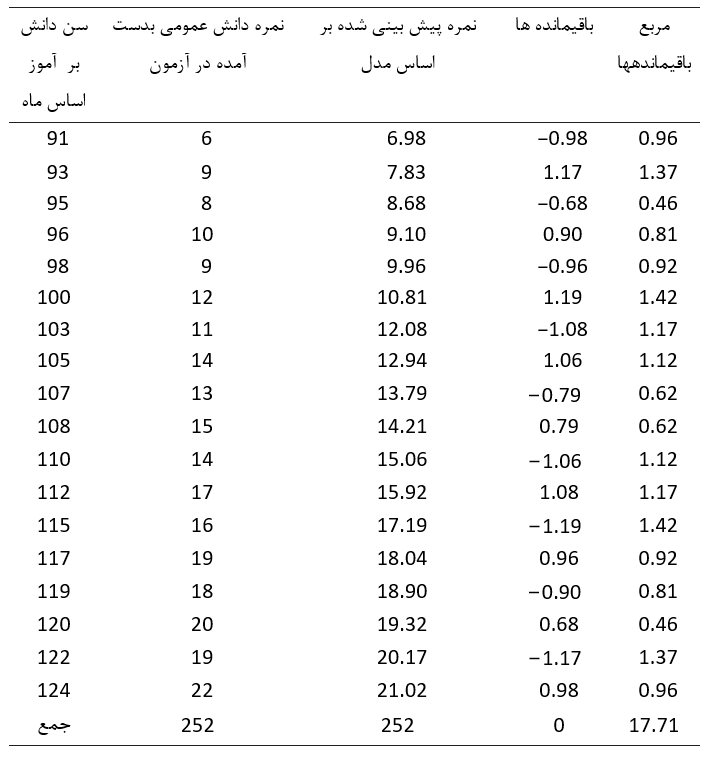
اولین نکته ای که باید به آن توجه شود این است که حاصل جمع باقیمانده ها صفر می شود؛ بدین معنی که باقیمانده های مثبت و برخی باقیمانده های منفی در نهایت با یکدیگر خنثی می شوند. علاوه بر این، مجموع مربعات باقیمانده ها (71/17) در این مدل از هر خط دیگر کمتر است.

انتخاب یک مدل خوب

دو معیار برای سنجش یک مدل خوب وجود دارد. اولین مورد این است که مدل از الگوی داده ها پیروی می کند. بدین معنی که اگر داده ها را بر روی نمودار ترسیم کنیم و از یک منحنی S-شکل پیروی کنند، در آنصورت دیگر خط مستقیم ممکن است مدل مناسبی نباشد. به عنوان مثال فرض کنید می خوایم بررسی کنیم آیا مدل خطی مدلی مناسب جهت برازش به داده ها است یا خیر. این جا است که باقیمانده ها نقش تعیین کننده خودشان را نشان می دهند. در واقع تصمیم گیری در مورد اینکه چه چیزی یک مدل خوب را ایجاد می کند و آیا این مدل برای برازش به داده ها مناسب است را نخست ویژگیهای باقیمانده ها تعیین می کند.

دوم اینکه مدل باید تا آنجا که ممکن است داده ها را تبیین کند و توضیح دهد. اگر مدل فقط بتواند 10 درصد از تغییرات نمرات را تبیین کند، ممکن است به خوبی مدلی که می تواند 90 درصد تغییرات را توضیح دهد، خوب نباشد. جنبه دوم را در بخش های بعد بررسی خواهیم کرد اما ابتدا ویژگی های باقیمانده ها را در نظر می گیریم.

ویژگی های باقیمانده ها

مدل خوب مدلی است که در آن خطا یا مقادیر باقیمانده تصادفی باشند. اگر مدل ما تغییراتی سیستماتیک در باقیمانده ها را به جا بگذارد، بدین معنی است که مدل بهتری نسبت به مدل پیشنهادی ما وجود دارد که قادر است این تغییر سیستماتیک را نیز در نظر بگیرد.

همچنین مدل برازش داده شده می بایست صرف نظر از مکان خاصی در داده ها، همواره به صورت یکسان داده ها را تبیین کند. چنانچه در چند نقطه اول مدل کاملاً منطبق بر داده ها باشد (منجر به باقیمانده های کوچک)، اما پس از آن با نقاط بعدی تناسب ضعیفی داشته باشد (منجر به باقیمانده های بزرگ)، مدل خوبی نیست. اینجاست که فرض برابری واریانس (یا هم واریانسی) لازم است: باقی مانده ها باید به طور تصادفی در هر نقطه از مدل که بررسی می کنیم، پراکنده شده باشند. بنابراین، پیش بینی می کنیم که واریانس باقیمانده ها در هر نقطه از مدل باید یکسان باشد – زیرا هیچ دلیل اصولی برای بزرگ بودن واریانس در یک نقطه نسبت به نقطه دیگر وجود ندارد.

برای حصول اطمینان از اینکه مدل ما الگوی مناسبی است و باقیمانده ها نیز کاملاً تصادفی هستند، سه فرض دیگر در مورد آنها ارائه می دهیم:

• حاصل جمع و میانگین آنها صفر است؛
• به صورت نرمال توزیع شده اند و
• از یکدیگر مستقل هستند.

ویژگیهای باقیمانده ها: حاصل جمع آنها صفر است.

با توجه به تجزیه و تحلیل بخش قبل متوجه شدیم تنها مدلی که حاصل جمع باقیمانده های آن صفر شود می تواند مدل خطی مناسبی برای داده ها باشد. یا به طور معکوس، اگر جمع باقیمانده ها صفر نشود، قطعاً مدل مناسب تری برای داده ها وجود دارد. در واقع صفر بودن حاصل جمع باقیمانده ها، تضمین می کند که مدل بر روی مقادیر متوسط داده ها طرح ریزی شده است.

ویژگیهای باقیمانده ها: توزیع آنها نرمال است

فرض کنید که مدل خطی به داده ها برازش داده شده است، در آن صورت خطاها (یعنی باقیمانده ها) می بایست تصادفی باشند و از یک توزیع نرمال پیروی کنند. اگر خطاها به طور تصادفی پراکنده شده باشند، در برخی موارد ممکن است باقیمانده های مثب بزرگی داشته باشیم و گاهی اوقات نیز امکان دارد باقیمانده های بزرگ منفی بدست آوریم، لذا در این موارد، بیشتر باقیمانده ها به صورت خوشه هایی در اطراف صفر جمع می شوند. بنابراین فرض نرمال بودن، فرض دیگری است که باقیمانده ها علاوه بر تصادفی بودن می بایست دارا باشند (و هیچ الگوی سیستماتیک در الگوی داده ها وجود ندارد که مدل حساب نکرده باشد). اگر باقیمانده ها از توزیع نرمال پیروی نکنند، مدلی که ما پیشنهاد داده ایم ممکن است مدل مناسبی برای این داده ها نباشد.

ویژگیهای باقیمانده ها: مستقل از هم هستند

اگر ارتباطی میان مقادیری باقیمانده ها و کودکان مورد آزمون یا کلاسی که از آن انتخاب شده اند، وجود داشته باشد، در آن صورت به نوعی می توان گفت باقیمانده هاغیرتصادفی هستند. اگر با افزایش سن کودکان باقیمانده ها نیز بزرگتر شوند دیگر باقیمانده ها از یکدیدگر مستقل نیستند. این مسئله نوعی نگرانی محسوب می شود، زیرا بیانگر رابطه ای در داده ها است که توسط مدل ارائه شده نشان داده نشده است.

بنابراین اگر باقیمانده ها از یکدیگر مستقل باشند، هیچ ارتباطی بین آنها وجود ندارد و بنابراین “خطایی” که پس از اعمال مدل تحمیل می شود یک مقدار تصادفی است و هیچ گونه تغییر سیستماتیک برای تبیین مدل باقی نمی گذارد. بنابراین یک مدل خوب، همه تغییرات سیستماتیک داده ها را توضیح می دهد و فقط تغییرات تصادفی را باقی می گذارد.

نتیجه گیری

اگر این مفروضات را برقرار نکنیم، ممکن است که باقیمانده ها کاملاً تصادفی نباشند و هنوز هم برخی تغییرات سیستماتیک در آنها وجود داشته باشد که می تواند توسط یک مدل جایگزین به حساب آید. در واقع فرض های رایجی که حین آزمون های آماری خود در نظر می گیریم (مانند همگنی واریانس و غیره) از این فرضیات مربوط به باقیمانده ها ناشی می شوند.

 

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا