آمار به زبان ساده – آزمون فرضیه با یک نمونه

آخرین به‌روزرسانی: 24 دی 1401

بعد از مطالعه فصل مقدمه ای بر آزمون فرضیه کتاب آمار به زبان ساده این فصل را با بررسی یک مثال شروع می‌کنیم.

یک مثال از آزمون فرضیه با یک نمونه

نشت گاز سایدامین از یک کارگاه تولید مواد شیمیایی در شهر نیوتن کاستل وابرهای ناشی از آن برای چند روز مردم این شهر را، پیش از آنکه بطور کامل در جو پراکنده شود، نگران نمود. شکایتی در میان مردم از درد گلو در این مورد وجود داشت اما شرکت شیمیایی مردم را مطمئن کرد که گاز سایدامین روی بدن انسان هیچ‌گونه اثر منفی ندارد. بهرحال یک دانشمند که روی پروژه سایدامین کار می‌کرد به سراغ سوابقی رفت که می‌گفتند این گاز می‌تواند روی زنان باردار و بچه‌هایی که در شکم آنان هستند تأثیر نامطلوب بگذارد.

شرکت شیمیایی ادعای این دانشمند را غیرمعقول خوانده و رد کرد و گفت این دانشمند نمی‌تواند مشخص کند که چه مشکلاتی برای این اشخاص می‌تواند بروز کند. در شرکت شیمیایی اطمینان همگانی وجود نداشت و در نواحی که مورد اصابت واقع شده بودند خصوصا از ناحیه والدین بچه‌های کوچک نگرانیهایی موجود بود. یک دکتر در بیمارستان بزرگ زنان و زایمان، بر روی بچه‌هایی که 9 ماه پس از واقعه ابرهای گازی که شهر را درنوردید، بدنیا آمده بودند متمرکز شد.

او متوجه شد که بچه‌ها در آزمایشهای معمول سالم بنظر می‌آیند اما شک کرد که گاز سایدامین وزن نوزادان را هنگام تولد کاهش میدهد. زیرا بسیاری از کودکان متولد شده کوچک بودند. این خانم دکتر نگران اثرات درازمدت بود و می‌خواست آزمایش کند که آیا بچه‌های سایدامین در هنگام تولد کوچکتر هستند یا خیر؟ بر این اساس دکتر پیش‌بینی یک دمی انجام داد: توزیع وزن زمان تولد کودکان تحت تأثیر سایدامین متفاوت از توزیع کودکان معمولی است. این توزیع روی انتهای پائینی توزیع کودکان معمولی قرار می‌گیرد.

برای آزمون این فرضیه، نیاز است جزئیات وزن زمان تولد دو جامعه را داشته باشیم. مقایسه این دو توزیع به ما خواهد گفت آیا اختلافی بین این دو وجود دارد، خصوصاً آیا میانگین وزن زمان تولد کودکان تحت تأثیر گاز کمتر از کودکان معمولی است؟ اما مشکل جمع‌آوری جزئیات دو جامعه است.

ممکن است در این زمینه خوش شانس باشیم، چون سوابق پزشکی با جزئیات زیاد موجود هستند و اجازه دهید فرض کنیم که آنها جزئیات وزن زمان تولد را دارند. ما از سوابق بچه‌هایی که در این منطقه به دنیا آمده‌اند درمی‌یابیم که میانگین وزن زمان تولد 2.3 کیلوگرم و انحراف استاندارد 9.0 کیلوگرم است. این جزئیات درباره کودکانی است که تحت‌تأثیر گاز سایدامین قرار نگرفته‌اند.

مشکل جمع‌آوری اطلاعات درباره کودکانی است که تحت‌تأثیر گاز سایدامین قرار گرفته‌اند. اساساً آنچه ما می‌خواهیم بدانیم آن است که جامعه کودکان معمولی چگونه تحت‌تأثیر سایدامین قرار خواهند گرفت؛ آیا بر روی آنها تأثیری خواهد گذاشت همانگونه که دکترها پیش‌بینی کرده‌اند که اثر سایدامین کاهش وزن زمان تولد همه به مقدار مشخصی است.

ما هرگز نمی‌توانیم جزئیات این جامعه را بدست آوریم، تمام آنچه داریم کودکانی از شهر نیوتن کاستل است که در زمان نشت گاز در شکم مادر خود بوده‌اند. این تنها یک نمونه از جامعه دوم است. نه فقط آن بلکه نمونه ما لزوماً نه نمایانگر جامعه و نه تصادفی است. نمی‌توان نمونه را آزادانه از جامعه تحت تأثیر گاز برگزید. نمونه‌های ما می‌تواند به همان اندازه سایدامین از فاکتورهای دیگر تأثیر بگیرند یا به جای گاز از چیزهای دیگر مثل تولد زودروس که موجب کاهش وزن است تأثیر گرفته باشند.

ما تصمیم می‌گیریم یکصد کودک را انتخاب کرده و توازنی میان آنها از جهت تولد در خانه یا در بیمارستان و محدوده سن جنین در هنگام نشت گاز و مانند آنها، برقرار کنیم تا تلاش کرده باشیم که نمونه برگزیده بصورت سیستماتیک با فاکتورهایی همچون عملیات بیمارستانی، سن جنین و غیره تحت تأثیر واقع نشده باشد.

ممکن است ما قادر نباشیم که همه تفاوتهای سیستماتیک که اثرات گاز سایدامین را روی نمونه و کودکان معمولی جدا می‌کند به حساب آوریم. اما می‌توانیم تمام تلاش خود را برای کنترل متغیرهای ابهام زای کلیدی انجام دهیم. اگر تفاوتی میان کودکان سایدامین و کودکان غیر آلوده یافتیم، ارزش خواهد داشت که برای اطمینان از اینکه آیا واقعاً تحت تأثیر گاز سایدامین بوده یا دلایل دیگر، تحقیقات بیشتری انجام دهیم. اگر تفاوتی یافت نشاید می‌توانیم تصمیم بگیریم که نیاز به تحقیقات بیشتری نیست.

ما وزن زمان تولد نمونه‌هایی از بچه‌های سایدامین را بدست آورده و میانگین نمونه را محاسبه می‌کنیم. عدد 0.3 کیلوگرم بدست می‌آید. آیا می‌توانیم این میانگین را با میانگین جامعه کودکان آلوده نشده معمولی مقایسه کنیم؟ پاسخ منفی است، زیرا دو چیز مشابه را مقایسه نمی‌کنیم و این احتمال اریبی را افزایش میدهد. برای تشریح این موضوع اجازه دهید چند لحظه جامعه معمولی را مورد ملاحظه قرار دهیم. همه کودکان در زمان تولد هم وزن نیستند، بعضی از آنها نسبت به سایرین بنا به پراکندگی نرمال وزن زمان تولد، سبکتر هستند.

حتی احتمال این مسئله وجود دارد که اگر نمونه‌ای از بچه‌های معمولی انتخاب کنید ممکن است وزن میانگین آنها کمتر از وزن میانگین جامعه باشد. که به صورت شانسی ممکن است که گروهی از کودکان را که نسبتاً سبکترند علیرغم این واقعیت که آنها از جامعه ای می‌آیند که میانگین وزن زمان تولد آنها بیشتر است انتخاب کرده باشیم.

ممکن است ما بچه‌های کوچکتر را انتخاب کرده باشیم (مطمئنم به همان صورت می‌توانید تصور کنید ممکن است نمونه‌ای با میانگین وزن زمان تولد بیش از میانگین جامعه برگزینیم). حتی اگر نمونه انتخاب شده ما از کودکان سایدامین، میانگینی پائینتر از کودکان معمولی نشان دهد، این را نمی‌توان به عنوان اثر گاز سایدامین بر وزن زمان تولد آنها تلقی نمود. این ممکن است به دلیل تفاوت جامعه نبوده و به آسانی بدلیل طبیعت نمونه‌گیری اتفاق افتاده باشد.

خوب اگر ما نتوانیم میانگین نمونه را با میانگین جامعه مقایسه کنیم پس چه می‌توانیم انجام دهیم؟ به یاد بیاورید که ما می‌توانیم یک نمره را با داشتن جامعه ای از نمرات مقایسه کنیم بنابراین نیازمندیم که میانگین نمونه را با جامعه ای از میانگین نمونه‌ها مقایسه نمائیم. اگر ما همه نمونه‌های ممکن 100تایی را از کودکان معمولی برگزیده و میانگین نمونه‌ها را بدست آوریم آنگاه می‌توانیم توزیعی از میانگین نمونه‌ها ایجاد کنیم.

بدین روش ما یک توزیع شناخته شده از میانگین نمونه‌های صدتایی از کودکان معمولی و یک توزیع ناشناخته یعنی توزیع میانگین نمونه صدتایی از کودکان جامعه آلوده، ایجاد کرده‌ایم. حالا می‌توانیم میانگین نمونه‌های دو جامعه را با یکدیگر مقایسه کنیم. اگر متفاوت باشند و میانگین توزیع کودکان آلوده کوچکتر باشد، فرضیه دکترها را تائید خواهیم کرد. متاسفانه ما هنوز جزئیات این جامعه‌ها را نداریم و تنها یک مقدار از جامعه ناشناخته یعنی میانگین نمونه صدتایی کودکان آلوده را در دست داریم.

اما آیا جزئیات توزیع میانگین‌ نمونه‌های 100تایی از کودکان معمولی را داریم، در اینجا پاسخ بلی است. نیازی نیست که بیرون رفته و از همه گروه‌های ممکن 100تایی از کودکان معمولی نمونه بگیریم زیرا ما میدانیم در توزیعهای نمونه‌گیری با اندازه بزرگتر از 30، توزیع میانگین‌ نمونه‌ها تقریباً قطعی یک توزیع نرمال است.

اکنون یک چهارچوب منطقی برای آزمون فرضیه ایجاد کرده‌ایم. ما یک نمره از یک توزیع ناشناخته در این مورد کودکان آلوده با میانگین 3 و یک توزیع شناخته شده یعنی توزیع نمونه‌گیری از نمونه‌های کودکان معمولی با همان اندازه داریم.

این توزیع به صورت نرمال با میانگین 2.3 و انحراف استاندارد 09.0 است. تمام آنچه نیاز است انجام دهیم عبارت است از برگزیدن یک سطح معنی داری برای فرضیه دکترها، یافتن نمره z، جستجو در جدول و یافتن احتمال و گرفتن تصمیم بر اینکه آیا نمونه آلوده از توزیعی مشابه نمونه کودکان معمولی بوده یا پائین‌تر از آن است.

ما در خواهیم یافت که احتمال نمونه‌ای از کودکان معمولی صدتایی با میانگین 3 را از طریق محاسبه مقدار z چقدر محتمل است .به یاد بیاورید که نمره z، یک مقدار منهای میانگین جامعه تقسیم بر انحراف استاندارد جامعه است. در اینجا میانگین

چون توزیع نمونه‌گیری ما یک توزیع استاندارد است می‌توانیم احتمال نمره Z آن را با نگاه کردن در جدول توزیع نرمال استاندارد بدست بیاوریم. به یاد داشته باشید که علامت منفی به آسانی به ما گوشزد می‌کند که نمره ما پائین‌تر از میانگین توزیع است. از جدول A.1 در ضمیمه a، نمره z 22.2 احتمالی برابر با 0132.0 به ما می دهد.

بنابراین احتمال بدست آمدن میانگین نمونه‌ای به کوچکی یا کوچکتر از 0.3 کیلوگرم از یک نمونه صدتایی کودکان معمولی فقط 0132.0 است. این به خوبی زیر 5 درصد از توزیع نمونه‌گیری کودکان معمولی و به خوبی زیر سطح معنی داری P=0.05 است. می‌توانیم نتیجه بگیریم که میانگین نمونه 0.3 کیلوگرم آنقدر در کودکان معمولی نایاب است که میانگین 0.3 کیلوگرمی نمونه کودکان آلوده ما دلالت بر آن دارد که این توزیع همان توزیع کودکان معمولی نبوده و فرضیه صفر را رد می‌کنیم، که حاصل آن خواهد بود که کودکان آلوده به گاز سایدامین در هنگام تولد وزن کمتری نسبت به معمولی دارند. این مسئله به صورت گرافیکی در تصویر 6.1 نشان داده شده است.

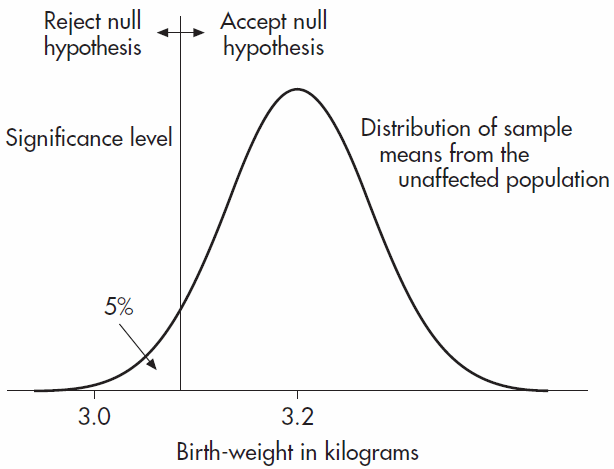
خلاصه آنچه گذشت

وقتیکه نمونه‌ای از یک جامعه ناشناخته داریم نمی‌توانیم آن را با یک جامعه شناخته شده مقایسه کنیم. باید میانگین نمونه،

با استفاده از این اطلاعات در مثالی که فرضیه را آزمودیم نشان داد که جایگاه توزیع ناشناخته از توزیع شناخته شده پایین تر است. از آنجا که توزیع شناخته شده یک توزیع نرمال است ما از نمره z برای یافتن احتمال اینکه میانگین توزیع شناخته شده به کوچکی و یا کوچکتر از میانگین توزیع ناشناخته باشد استفاده می کنیم. چون احتمال بدست آمده کوچکتر از سطح معنی داری است، فرضیه صفر را رد کرده و نتیجه می‌گیریم که جایگاه توزیع ناشناخته کوچکتر از توزیع شناخته شده است: یعنی بچه‌های آلوده به گاز سایدامین در هنگام تولد وزن کمتری از بچه‌های معمولی دارند.

وقتیکه انحراف استاندارد جامعه را در دست نداریم

متوسط خرید در یک سوپر مارکت 25 قلم است. شرکت (صاحب فروشگاه) می‌خواهد این رقم را افزایش داده و یک سلسله فعالیت تبلیغاتی برای تشویق خریداران به خرید بیشتر محصولات فروشگاه به راه اندازد. یک هفته بعد از تبلیغات 50 خریدار مورد آزمایش قرار گرفتند تا روشن شود تعداد خریدها افزایش یافته است یا خیر. از آنها تعداد خریدهای زیر ثبت شده است.

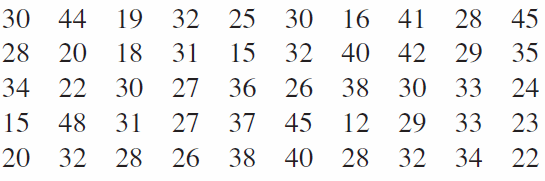
میانگین تعداد خرید این نمونه 30 قلم و انحراف استاندارد نمونه 43.8 است.

آیا فعالیت‌های تبلیغاتی تأثیری داشته است؟ همانگونه که در بالا می‌بینید ما نمی‌توانیم میانگین نمونه پس از تبلیغات خریداران را (30 قلم) با میانگین جامعه پیش از تبلیغات خریداران (25قلم) مقایسه کنیم زیرا یکی نمونه و دیگری یک جامعه است. برای مقایسه میانگین نمونه با توزیع میانگین‌ نمونه‌ها، می‌بایستی توزیع نمونه‌گیری میانگین نمونه‌ها به همان سایز 50 تایی از خریداران پیش از تبلیغات را محاسبه کنیم. این توزیع میانگین (زیرا به همان اندازه میانگین

متأسفانه، در اینجا گیر می‌افتیم، زیرا در این حالت را یعنی انحراف استاندارد جامعه خریداران پیش از تبلیغات را نداریم. برای ادامه باید را تخمین بزنیم. فرض می‌کنیم که تأثیر فعالیتهای تبلیغاتی، بالا بردن رتبه کل توزیع فروشهاست: یعنی پس از فعالیتهای تبلیغی میانگین جامعه بالاتر بوده (افراد اقلام بیشتری خریداری می‌کنند) اما انحراف استاندارد به همان شکل باقی می‌ماند (پراکندگی تعداد خریدها به همان شکل قبل است) تنها انحراف استانداردی که ما داریم، انحراف استاندارد نمونه پس از تبلیغات s است.

انحراف‌ استاندارد نمونه،مقداری پایدار بوده و به خوبی مقدار موجود در جامعه در جامعه را برآورد می کند بنابراین می‌توانیم این را برای برآورد کردن انحراف استاندارد جامعه پس از تبلیغات استفاده کنیم.

از آنجائیکه فرض می‌کنیم انحراف استاندارد جامعه پس از تبیلغات، با پیش از تبلیغات یکسان است، می‌توانیم انحراف استاندارد نمونه خود sرا بعنوان یک تخمین از انحراف استاندارد جامعه پیش از تبلیغات به کار ببریم (چون ما پیش‌بینی کردیم که اثر تبلیغات رتبه توزیع را بالاتر برده ولی به هرحال شکل آن را تغییر نمی‌دهد و لذا انحراف استاندارد به همان اندازه باقی می‌ماند).

برای به کار بردن انحراف استاندارد نمونه بعنوان برآوردی از پارامتر جامعه، باید تقبل کنیم که هیچگونه اریبی ای در نمونه ما رخ نداده است مثلاً فقط از خریداران پولدار بوده و یا نمی‌تواند برآورد خوبی باشد. بنابراین فرض می‌کنیم نمونه ما بصورت تصادفی از جامعه پس از تبلیغات انتخاب شده است. اگر این مفروضات درست باشد آنگاه انحراف استاندارد نمونه یک برآورد قابل قبولی از مقدار جامعه پیش از تبیلغات خواهد بود.

برای مشخص نمودن اینکه ما انحراف استاندارد جامعه یعنی را نداشته و به جای آن از S برای برآورد استفاده کرده، به جای استفاده از آماره Z، آماره جدید را t می‌نامیم.

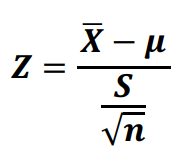
انحراف استاندارد نمونه فرمول زیر را دارد:

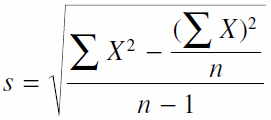
با جایگزین کردن مقدار S در فرمول t، فرمول جدید زیر را برای t خواهیم داشت:

توجه کنید که t بوسیله درجه آزادی نمونه تحت تأثیر قرار گرفته است(n-1). این بخاطر آن است که t همان Z نیست، بلکه برآوردی از اوست. وقتیکه درجه آزادی کوچک باشد توزیع t مشابه توزیع نرمال ولی صاف‌تر و پراکنده‌تر است.

همانطور که درجه آزادی بزرگتری شود توزیع t به سرعت به توزیع نرمال نزدیک شده و زمانیکه درجه آزادی برابر بی‌نهایت باشد، مشابه توزیع نرمال خواهد بود. تصویر 602 سه توزیع t با 1 و 10 و بی‌نهایت درجه آزادی را نشان می‌‌دهد. حتی در 10 درجه آزادی توزیع t بسیار شبیه توزیع نرمال است و در 30 درجه آزادی و بالاتر از آن تفاوتها آنقدر کوچک هستند که قابل نادیده‌ گرفتن می‌باشند.

ما همیشه در جدول توزیع نرمال استاندارد به دنبال نمره Z می‌گردیم. با t این کار را نمی‌توان انجام داد چون t یک توزیع نرمال نیست. ولی بهرحال همانند جدول توزیع نرمال استاندارد، مقادیر توزیع t استخراج شده است. مسلم است که آنها برای مقادیر متفاوت توزیع t مطابق با درجه‌های مختلف آزادی بدست آمده‌اند. می‌توانیم برای مقدار t محاسبه شده خودمان در جدول به دنبال توزیع مناسب گشته و احتمال اینکه این مقدار از یک توزیع شناخته شده باشد را بیابیم.

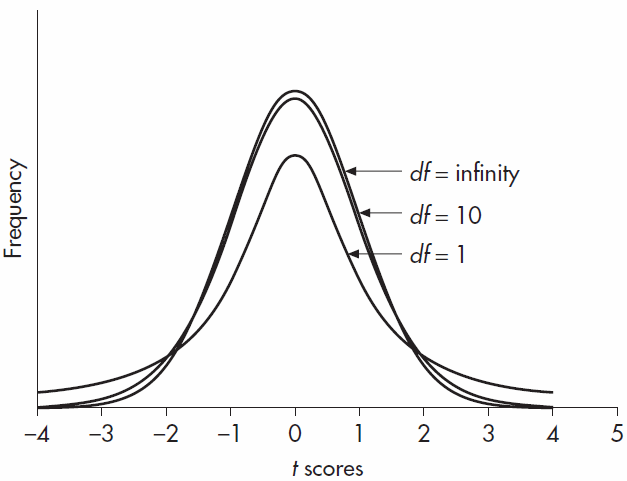
مثال هایی از توزیع t

می‌توان این مقدار را با سطح معنی داری مقایسه کرد و تصمیم گرفت که فرضیه صفر را پذیرفته یا آنرا رد می‌کنیم. بنابراین می‌توانیم درگیر آزمون فرضیه ای شویم که نمونه ای داشته، حتی زمانیکه انحراف استاندارد جامعه شناخته شده را نمی‌‌دانیم.

برای انجام آزمون t باید سه فرض را بپذیریم:

• توزیع شناخته شده به صورت نرمال توزیع شده است. این مهم است زیرا (همانند نمره Z) نیاز داریم که توزیع نمونه‌گیری ما به صورت نرمال باشد. اگر چنین نباشد توزیع t در جدول نمی‌تواند ارقام مناسب را برای تصمیم‌گیری در مورد معنادار بودن مقدار t که محاسبه کرده‌ایم به ما بدهد. اما بهرحال اغلب تصریح می‌شود که آزمون t نیرومند است، این اصطلاح اهالی آمار است برای اینکه بگویند حتی اگر توزیع نمونه‌گیری پایه، توزیع نرمال نباشد، آزمون t ممکن است همچنان ارقام قابل قبولی برای مقایسه مهیا کند. توزیع جامعه پایه هرچه می‌خواهد باشد، به طور قطع وقتیکه اندازه نمونه 30 یا بزرگتر باشد، توزیع نمونه‌گیری بسیار نزدیک به نرمال است.
• نمونه به صورت تصادفی از جامعه (ناشناخته) گرفته شده است.زیرا می‌خواهیم انحراف استاندارد نمونه، برآوردی بدون اریبی از انحراف استاندارد جامعه و بنابراین برآوردی مناسب برای به کار بردن باشد، در غیر اینصورت بر محاسبه t تأثیر خواهد گذاشت.
• انحراف استاندارد جامعه ناشناخته، مشابه همان انحراف استاندارد جامعه شناخته شده است. تنها در صورت پذیرفتن این فرض است که می توانیم انحراف استاندارد نمونه را به عنوان برآوردی از انحراف استاندارد جامعه شناخته شده به کاربریم .

به مثال خود بازگشته و می‌گوئیم تا زمانیکه دلیلی بر اینکه «نمونه 50 تایی خریداران ما به طور اریب انتخاب شده باشند» وجود ندارد فرض‌های بالا برای مقرر شدن در اینجا معقول است . اکنون می‌توان t را برای یافتن احتمال وجود یک نمونه پیش از تبلیغات با میانگینی به بزرگی 30، محاسبه کنیم.

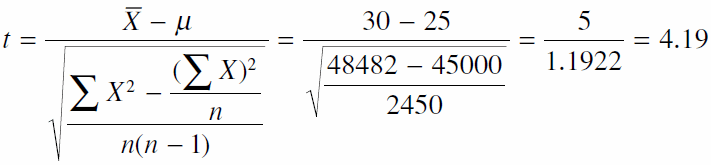
طبعاً درجه آزادی را باید محاسبه کنیم.

49= 1- 50 = 1 – n

اگر به جدول مقادیر t در ضمیمه A.2 نگاه کنیم، متوجه خواهیم شد که برخلاف جدول نرمال استاندارد، این جدول همه مقادیر توزیع را ندارد چون در آن صورت می‌بایست برای دادن مقادیر هر توزیع متفاوت t، جدول پشت جدول می‌ساختیم. آنچه در این جدول موجود است مقادیر کلیدی برای هر توزیع بوده و به شکلی که مقادیر کلیدی، مقادیر t در سطح معنی دار بودنی است که برگزیده‌ایم یعنی کدام مقدار t به طور دقیق 5 درصد از احتمال و کدام مقدار 1 درصد از احتمال کل توزیع t را جدا می کند.

ما یک آزمون یک دمی داشتیم (که پیش‌بینی کردیم برنامه‌های تبلیغاتی در فروش بیشتر موثر بوده است). با استفاده از سطح معنادار بودن P=0.05، نگاهی به پائین ستون P=0.05 انداخته و به دنبال ردیف درجه آزادی 49 درجه می‌گردیم، اما می‌بینیم که مقدار t برای آن موجود نیست. رقم 684.1را برای درجه آزادی 40 و 671.1 برای 60 درجه آزادی در آن‌جا وجود دارد. مجدداً تکرار می‌کنیم دلیلش این است که اگر می خواستیم برای همه اعداد مقدار ذکر کنیم این ستونها تا ابد باید ادامه می‌یافت.

می ببینیم که بین این دو مقدار تفاوت زیادی وجود ندارد (013.0) بنابراین به طور اجمالی می‌دانیم که مقدار 49 درجه آزادی جایی بین آن دو است (671.1 و 684.1). با روشی که تناسب خطی نامیده می‌شود و ساده‌تر از آن چیزی که بنظر می‌آید است آن را محاسبه می کنیم. بین 40 و 60 یک فاصله 20تایی و بین 684.1 و 671.1 یک فاصله 013.0 است.

بنابرای برای هر درجه آزادی بین 40 تا 60، در جدول مقدارئ 20 / 0.013 تفاوت وجود دارد که برابر 00065.0 می‌شود برای 9 درجه آزادی فاصله برابر 00585.0 = 00065.0 × 9 خواهد شد. از این رو برای 49 درجه آزادی، در جدول مقدار t برابر 00585.0 – 684.1 بوده که حاصل آن 67815.1 است. (اگر مایل به تناسب گرفتن نیستید از میان دو عدد جدول، عدد بزرگتر را بگنجانید).

از آنجائیکه مقدار t ما که برابر 67815.1 است با 49 درجه آزادی دقیقاً 5 درصد از احتمال زیر نمودار t را جدا می کند، و اگر مقدار t بزرگتر شود، ناحیه کوچکتری از انتهای توزیع یا دم را قطع خواهد نمود، احتمال بدست آوردن مقدار t معادل 19.4 از توزیع شناخته شده کمتر از 5 درصد است بنابراین می‌توانیم فرضیه صفر را رد کرده و برای متفاوت بودن دو توزیع استدلال کنیم.

ساد‌ه‌تر از آن می‌توانیم نتیجه بگیریم از آنجائیکه مقدار محاسبه شده ما برای 19.4 با 49 درجه آزادی بزرگتر از مقدار 67815.1 است، و برای یک آزمون یک طرفه در سطح معنی داری P=0.05 افزایش قابل توجهی در اقلام خرید پس از برنامه‌ تبلیغاتی وجود دارد. توجه کنید حتی در سطح معنی داری محافظه‌کارانه‌تر P=0.01 این مقدار قابل توجه است. معمولاً یافته‌ها در سطح معنی داری پائین‌تر را دلیل بر غیر محتمل بودن ایجاد این اثر بصورت شانسی ذکر می‌کنند. (می‌توانید با استفاده از تناسب مقدار جدول t برای 49درجه آزادی در سطح معنی داری P=0.01 را بدست آورید. قطعاً مقدار بدست آمده شما t=2.40815 خواهد بود).

فواصل اطمینان

آزمون t، آزمونی برای معنادار بودن است و ما براساس اطلاعات ساده‌ای که داریم شواهد را برای بررسی یک اختلاف معنادار آماری بین جوامع جستجو می‌کنیم. روش دیگر به کار بردن اطلاعات نمونه برای برآورد کردن پارامترهای جامعه است. اکنون ممکن است بگوئید که قبلاً این کار را با استفاده از مقدار میانگین نمونه برای برآورد مقدار جامعه انجام داده ایم. این صحیح است اما می‌توانیم با بدست آوردن فاصله اطمینان برای میانگین کمی پیشرفته‌ تر عمل کنیم.

افزون بر انتخاب یک مقدار برای میانگین جامعه، می‌توانیم محدوده‌ای از مقادیر را که مطمئن هستیم آن مقدار در آن وجود دارد، مشخص کنیم. سطح اطمینان را معمولاً 95 یا 99 درصد اطمینان، انتخاب کرده، آنگاه محدوده مقادیر را بدست می‌آوریم. با فاصله اطمینان 95 درصدی، می‌گوئیم که اگر ما فاصله اطمینان برای 100 نمونه مختلف از یک جامعه را بدست آوریم آنگاه 95 درصد از آن فاصله‌های اطمینان باید حاوی مقدار میانگین جامعه باشند. بنابراین فاصله اطمینان، برآورد خوبی برای مشخص کردن مکان وجود میانگین واقعی است.

در مثال بالا به سادگی می‌توانیم فاصله اطمینان 95 درصدی را بدست آوریم همانگونه که از اطلاعات تولید شده خودمان برای بدست آوردن t استفاده کردیم. زیرا در آزمون t فاصله اطمینان (CI) به شکل زیر مشخص شده است.

(خطای استاندارد میانگین × نقطه بحرانی t) ± میانگین نمونه = CI

در این حالت مقدار بحرانی t، آنی است که 95 درصد مرکز توزیع را در بر می‌گیرد و فقط 5 درصد خارج از این محدوده باقی می‌ماند و مقدار دو طرفه t از جدول که در آن p=0.05 باشد، محدوده‌ای 025.0 از هر طرف توزیع جدا می کند درجه آزادی ما 49 درجه است بنابراین می‌توانیم مقدار بحرانی t را از جدول استخراج کرده که مقدار آن016.2 است. (بوسیله تناسب خطی بین df=40 و df=60). می دانیم که میانگین نمونه 30 و خطای استاندارد میانگین (برآورد شده) 922.1 است (زیرا بخش پائینی فرمول آزمون t است) بنابراین داریم:

3982.2 ± 30 = 1922.1 × 0116.2 ± 30 = CI %95

که به ما میدهد

(3982.32 و 6018.27) = CI %95

این نشانه سودمندی از موقعیت واقعی میانگین جامعه است. هرچه فاصله اطمینان کوتاهتر باشد تخمین ما از میانگین جامعه دقیق‌تر خواهد بود. در اینجا مطمئن هستیم که میانگین جامعه بین 6018.27 و 3982.32.قرار دارد حتی کمترین مقدار این دو محدوده هنوز بخوبی بالای مقدار 25 قلم خرید قبل از تبلیغات است.

می‌توان از آنالیز فاصله اطمینان خود برای بدست آوردن فواصل اطمینان برای مقدار میانگین قبل و بعد از تبلیغات استفاده کنیم. از همان فرمول استفاده کرده ولی میانگین نمونه را با اختلاف میانگین‌ها عوض می‌کنیم.

(انحراف استاندارد اختلاف میانگین‌ها × مقدار بحرانی t) ± اختلاف میانگین‌ها = CI

مقدار بحرانی t و خطای استاندارد همانها هستند که در محاسبه قبلی به کار بردیم و مقدار را هم می‌دانیم بنابراین:

 (1922.1 × 0116.2) ± (25 – 30) =CI %95

(3982.7 و 6018.2) = CI %95

این به ما محدوده‌ای از مقادیر را داده که مطمئن هستیم (95 درصد اوقات) حاوی اختلاف در جامعه است. توجه کنید که در بدترین حالت (حد پائین‌تر) انتظار 60.2 فروش بیشتر را بعد از تبلیغات داریم، بنابراین می‌توانیم مطمئن باشیم که تبلیغات اثر داشته است. اگر حد پائین‌تر صفر یا منفی باشد قادر نخواهیم بود که اثر مشخصی را برای تبلیغات فرض کنیم زیرا اختلاف واقعی صفر خواهد بود.

ساختار عمومی یک فاصله اطمینان

فاصله اطمینان بالا با استفاده از آماره های ساده (میانگین، تفاوت میانگین‌ها)، اطلاعات ساده (خطای استاندارد) و توزیع آماری مناسب داده‌ها (توزیع t) حاصل شده است. فاصله اطمینان برای بسیاری از تحلیلهای آماری را می‌توان با همان ساختار بالا محاسبه نمود ولی دستور کلی را به شکل زیر می‌نویسیم:

خطای استاندارد آماره × مقدار بحرانی توزیع مقتضی ± مقدار آمار = CI

پس از آن نیاز است که قلم آماری مناسب، مقدار بحرانی و خطای استاندارد برای محاسبه فاصله اطمینان را برگزینیم، همانطور که در بالا دیدیم آماره را بدست آورده و خطای استاندارد داده خود را برآورد می کنیم و سطح اطمینانی را که مایلیم برمی‌گزینیم (90 یا 95 درصد)، آنگاه مقدار بحرانی درست را برای آن سطح اطمینان انتخاب می‌کنیم.

فواصل اطمینان و معنی داری

آزمونهای معنادار بودن و فاصله‌های اطمینان هر دو قصد دارند که به یک پرسش پاسخ دهند:

اطلاعات نمونه ما درباره مقدار جامعه چه می‌گویند و از آن چه چیزی را می‌توانیم استنتاج کنیم؟

در مورد اول، یعنی آزمون معنادار بودن، در جستجوی آن هستیم که آیا آماره از یک معیار ویژه (سطح معنی داری p=0.05) فراتر می‌رود تا مدعی معنادار بودن آن آماره شویم (و فرضیه صفر را رد کنیم). در مورد دوم، یعنی فاصله اطمینان، در جستجوی، یافتن محدوده‌ای هستیم که در آن مطمئن باشیم که مقدار جامعه در آن موجود است. اگر به سطح اطمینان یک تفاوت نظر بیفکنیم می‌توان این محدوده را به نسبت صفر آزموده تا به ما نشانه‌ای بدهد که آیا فکر می‌کنیم این تفاوت مهم است یا خیر.

اگر فاصله اطمینان شامل صفر باشد آنگاه تفاوت برای مقادیر جامعه صفر خواهد بود و بدین دلیل هر تفاوتی که در میانگین‌های نمونه‌ها بیابیم اهمیتی نخواهد داشت.

آزمون معنادار بودن به صورت سنتی در تعدادی از بخش‌های آنالیز داده‌ها به کار میرود.اما استفاده ازفاصله اطمینان به صورت روز افزونی در حال افزایش است.

این بخاطر آن است که آزمون معنادار بودن یک خروجی «این یا آن» دارد یعنی یا فرضیه صفر مردود می‌شود و یا آن در یک سطح خاص معنادار نیست، در حالیکه فاصله اطمینان محدوده‌ای از مقادیر را که برآورد سودمندی از اندازه تفاوت بوده را به ما عرضه می‌کند. در حقیقت آزمونهای معنادار بودن و فاصله‌های اطمینان مکمل یکدیگر در آشکار کردن یک تصویر واضح‌تر از داده‌ها هستند فراتر از آنچه ممکن است به تنهایی قادر به آن باشند.

در بسیاری از حالات (با یافته‌های بسیار قابل ملاحظه‌ای بطور مثال) نتیجه‌گیری روشن است اما جائیکه یافته‌ها نزدیک به معنادار بودن باشند (مثلا با احتمال 06.0، که می‌توانیم بگوئیم معنی دار نیست) فاصله‌های اطمینان به ما کمک می‌کنند که ارزش تحقیقات بیشتر را سنجیده، بویژه اگر، تعدادی فاکتور موثر بر خروجی آمار ما موجود باشد.

نتیجه‌گیری

خواه یک نمونه و خواه یک نمره جداگانه را بیازمائیم، همان منطق اعمال خواهد شد. به هر حال با استفاده از نمونه «نمره از توزیع ناشناخته » به میانگین نمونه از توزیع نمونه گیری ناشناخته تبدیل می شود و ما آن را با میانگین نمونه های توزیع شناخته شده که از نمونه هایی با همان اندازه به دست آمده اند، مقایسه می کنیم. وقتیکه جزئیات نمره و توزیع شناخته شده را داشته باشیم آنگاه روال کار یکسان است: مقدار Z را بدست آورده و احتمال آن را پیدا می‌کنیم تا تصمیم بگیریم که فرضیه صفر را پذیرفته یا آن را رد کنیم.

اگر انحراف استاندارد جامعه شناخته شده را نداشته باشیم این کار کمی پیچیده‌تر خواهد بود اما زمانیکه فرض مناسبی را بپذیریم می‌توانیم انحراف استاندارد نمونه را برای تقریب آن به کار ببریم. آنگاه به جای z، t را محاسبه می‌کنیم. از آنجائیکه تمامی مقادیر t بدست آمده است می‌توانیم بدنبال مقدار t با درجه آزادی متناسب، برای انتخاب سطح معنادار بودن بگردیم. اگر مقدار محاسبه شده ما از مقدار جدول بزرگتر بود می‌توان فرضیه صفر را رد کرد.

فاصله‌های اطمینان راه جایگزینی برای نمایش یافته‌هایمان عرضه می‌کند زیرا محدوده‌ای از مقادیر را که مطمئن هستیم مقدار جامعه در آن است به ما میدهد. این را می توان به عنوان راه جایگزین برای آزمون معنادار بودن برگزیده یا آن را به عنوان اطلاعات تکمیلی برای آن تلقی کنیم.

 

مترجمین: دکتر هدی کامرانی فر – حسن اسکندری نیا